Listas
E mais: tuplas
Até aqui aprendemos vários tipos de dados: int, float, bool,
str. O que todos esses tipos tem em comum é que eles são simples,
básicos. Hoje vamos aprender tipos de dados compostos: tuplas e
listas. Chamamos tuplas e listas de tipos compostos porque
teoricamente elas não são um tipo sozinhas: elas são sempre
tuplas/listas de alguma coisa (listas de números, listas de listas de
strings, etc).
1. Tuplas
Tuplas são uma generalização de duplas/pares; podemos ter triplas, quádruplas, etc. Representamos tuplas por parênteses, com cada elemento da tupla separado por vírgulas:
empty_tuple = () interval = (0, 1)
Acessamos valores de tuplas de duas formas. Uma delas nós já conhecemos de outra aula: quando retornamos múltiplos resultados de uma função é como se estivéssemos retornando uma tupla, e portanto podemos usar a mesma sintaxe de assignment para desestruturar (‘desmontar’) a tupla.
interval = (0, 1) beg, end = interval
A outra forma é por meio de indexação, especificando diretamente o índice do elemento que queremos. Como de praxe, a contagem do índice começa do zero (e portanto o índice do último elemento de uma tupla de \(n\) elementos é \(n-1\)):
full_name = ("Guido", "van Rossum") first_name = full_name[0] surname = full_name[1]
Como se vê, para fazer uma indexação nós colocamos colchetes depois do que queremos indexar, com o número do índice dentro dos colchetes.
Nada impede que usemos uma variável para indexar, mas é preciso que o valor dela seja um inteiro:
i = 2 student_info = ("Jack Black", "5906-94", 67.9) grade = student_info[i]
Uma grande utilidade de tuplas é em fazer assignments múltiplos. Quando queremos trocar o valor de duas variáveis (um swap) sem usar tuplas, precisamos criar uma terceira variável não relacionada:
a = 0 b = 1 # swap! tmp = b b = a a = tmp
Com tuplas e assignment múltiplo, podemos fazer simplesmente:
a = 0 b = 1 # swap! (b, a) = a, b
Isso funciona pois do lado direito do = ainda temos os valores
antigos de a e b. Se tentássemos separar os assignments
perderíamos um dos valores:
a = 0 b = 1 # swap! b = a a = b # aqui a == b == 0
2. Listas
O tipo de dados lista também é intuitivo, sendo uma sequência de elementos acessível por índice (indexável). Listas em geral contém um tipo só (listas de inteiros, listas de tuplas de string e números, etc).
empty_list = [] finite_fibonacci = [0, 1, 1, 2, 3, 5, 8] len(finite_fibonacci) # calcula o ‘comprimento’ da lista, seu número # de elementos finite_fibonacci[4] # == 3
Como podemos ver, uma lista é declarada por um par de colchetes, e seus elementos vão dentro dos colchetes, separados por vírgulas. Não há confusão possível com a sintaxe de indexação, veja:
grades = [8.8, 7.5, 0, 9.4] print(grades[2]) # alguém faltou à prova… print(["hey", "you"][1])
O grande diferencial de listas é que elas são mutáveis (assim como variáveis), e extensíveis (seu tamanho pode crescer ou diminuir).
grades = [8.8, 7.5, 0, 9.4] grades[2] = 6.7 # substituindo com a nota da segunda chamada print(grades) grades = grades + [5.5, 7.1, 8.3] # adicionando notas de outra turma # da mesma disciplina print(grades)
Outro ponto interessante de listas é que podemos iterar sobre elas:
sum_total = 0 grades = [8.8, 7.5, 0, 9.4] for i in range(len(grades)): sum_total = sum_total + grades[i] average = sum_total / len(grades)
Mas na verdade, a melhor forma de iterar sobre uma lista é sem usar range:
sum_total = 0 grades = [8.8, 7.5, 0, 9.4] for grade in grades: sum_total = sum_total + grade average = sum_total / len(grades)
Desta forma não precisamos de usar os índices desnecessariamente, e
portanto é impossível de errá-los, começando a iteração do índice
errado, ou acabando antes do último elemento, ou tentando acessar um
elemento que não existe (tente fazer ["hello", "there"][2]).
2.1. Exercício: variância
Crie uma função chamada variance que recebe uma lista de números e
calcula a variância populacional deles, dada por \(\sigma^2\).
\[\sigma^2 = \frac{1}{N}\sum_{i=1}^{N} (x_i - \mu)^2 \qquad \mu = \frac{1}{N}\sum_{i=1}^{N} x_i\]
3. Operadores e funções de listas
Como vimos em exemplos anteriores, podemos usar a função len para
determinar o tamanho ou comprimento de uma lista (seu número de
elementos). Também podemos usar o operador de adição (+) para fazer
uma lista maior. Além disso, o operador in que usamos para fazer um
loop sob uma lista (for element in my_list) também pode ser usado
sozinho (sem o for) para checar se um valor está presente na lista,
retornando o valor booleano (True ou False) correspondente:
if "needle" in ["hay", "more hay", "needle", "even more hay"]: print("Found it!") print(3.141592 in [3, 3.1, 3.14, 10])
Nem len nem in são operadores exclusivos de listas (mais
para a frente veremos mais usos para eles), mas existem uma série de
funções que podem ser aplicadas somente à listas:
fila = ["Michael", "Dwight", "Angela"] list.pop(fila) # remove e retorna o último elemento da lista list.sort(fila) # ordena os elementos da lista list.append(fila, "Jim") # adiciona um novo elemento ao final da lista
Como se vê, essas funções todas são começam com list., por conta de
sua exclusividade para listas. Para economizar digitação, Python nos
permite omitir o prefixo list da seguinte forma:
fila = ["Michael", "Dwight", "Angela"] fila.pop() # remove e retorna o último elemento da lista fila.sort() # ordena os elementos da lista fila.append("Jim") # adiciona um novo elemento ao final da lista
Isso só funciona se o que vier antes do ponto de fato for uma lista, e
nesse caso fila.append("Jim") e list.append(fila, "Jim") são
equivalentes (se fila não for uma lista, teste e veja o que acontece
em cada caso).
Ao rodar esse pedaço de código, o que você espera que seja o valor
final de lista fila? Até aqui, se nós fizermos uma operação como
x + 1 e não fizermos o reassignment (como em x = x + 1), o valor
calculado é perdido, descartado. Mas ao averiguarmos o valor de fila
depois das operações acima, ele mudou.
3.1. Exercício: produto cartesiano
Crie uma função chamada cartesian_product que recebe duas listas e
produz uma nova lista que seja o produto cartesiano entre elas. Para
fazer o produto em si, utilize tuplas; de modo que se \(n\) é membro da
primeira lista e \(m\) é membro da segunda lista, então \((m, n)\) é
membro da lista-resultado.
Por exemplo, uma implementação correta de cartesian_product teria o
seguinte comportamento (mas a ordem dos elementos da lista pode ser
diferente):
print(cartesian_product([1,2], [3,4])) # [(1,3), (1,4), (2,3), (2,4)] print(cartesian_product([], [3,4])) # [] print(cartesian_product([1], [2, 3])) # [(1,2), (1,3)]
4. Funções puras e funções com efeito colateral
def append_pure(ls, elem): return ls + [elem] def append_impure(ls, elem): ls.append(elem) return ls # compare: languages_i_love = [] print(append_pure(languages_i_love, "Spanish")) print(languages_i_love) print(append_impure(languages_i_love, "Python")) print(languages_i_love)
Em Python e em outras linguagens de programação, algumas funções e
comandos são puros, ao passo que outros são impuros ou tem
efeitos colaterais. Calcular languages_i_love + ["Spanish"] não
tem nenhum efeito colateral — nenhuma variável é modificada, não há
nada printado na tela, etc. Por conta disso, se não fizermos um
assignment languages_i_love = languages_i_love + ["Spanish"] o valor
calculado será descartado. Funções como list.append tem efeito
colateral; além de avaliarmos seus argumentos (uma lista e um valor a
ser inserido nela), modifica-se a lista como ‘efeito’. print é
impura, pois tem o efeito colateral de mostrar algo na tela.
Uma função pura, assim como uma função matemática, sempre tem o mesmo
resultado para as mesmas entradas, e não modifica nem as entradas nem
nenhuma outra variável. Se languages_i_love = [], podemos invocar
append_pure(languages_i_love, "Spanish") 5 vezes e o resultado será
sempre ["Spanish"], ao passo que languages_i_love continua sendo
[]. Para uma função impura, as mesmas entradas de uma função podem
trazer resultados diferentes; basta invocar
append_impure(languages_i_love, "Python") mais de uma vez e ver como
o resultado é sempre diferente; isto acontece porque o valor de
languages_i_love está sendo modificado a cada chamada da
função. Teste você mesmo!
4.1. Descobrindo mais sobre uma função
Uma pergunta natural é como saber se uma função tem efeito
colateral. Se você está usando uma função que não foi você que
escreveu (por exemplo uma função que é built-in do Python como
list.sort), quem escreveu a função deve ter informado se as
propriedades da função, se ela tem efeitos colaterais, se modifica
seus argumentos, etc. Podemos usar a função help no shell Python
para ver a documentação de funções Python:
help(list.sort)
nos diz (entre outras coisas)
The sort is in-place (i.e. the list itself is modified) and stable (i.e. the order of two equal elements is maintained).
O que nos esclarece que list.sort modifica a lista. Se fizermos
help(sorted), vemos que
Return a new list containing all items from the iterable in ascending order.
Ao dizer que retorna uma lista nova, entende-se que a anterior não é modificada, e portanto a função é pura.
Ao escrever nossas próprias funções nós podemos escolher se queremos que elas sejam puras ou não. Podemos informar isso e outras propriedades da função (além de explicações em geral) colocando uma string (chamada docstring) após a definição do nome da função e de seus argumentos, como no exemplo abaixo:
def append_pure(ls, elem): """Retorna um nova lista com um elemento adicionado à seu fim. Argumentos: ls -- lista elem -- elemento a ser adicionado ao final da lista """ return ls + [elem] help(append_pure)
Como se pode ver, help pode ser usado em funções que nós mesmos
definimos, e o texto que adicionamos como docstring será também
mostrado. help é prática de ser usada, mas também podemos encontrar
essas e outras informações sobre uma função built-in de Python na
documentação oficial (exemplo para sorted).
5. Mutabilidade e imutabilidade
Como mencionamos anteriormente, listas são mutáveis. Mas além de
podermos modificar seus elementos, há uma outra consequência; veja a
comparação abaixo com um tipo imutável (int).
n = 42 answer = n n = n + 1 print(n, answer) languages_i_love = [] languages_i_like = languages_i_love languages_i_love.append("Python") print(languages_i_love, languages_i_like) languages_i_like = languages_i_like + ["Dothraki"] # O que você acha que será o resultado? print(languages_i_love, languages_i_like)
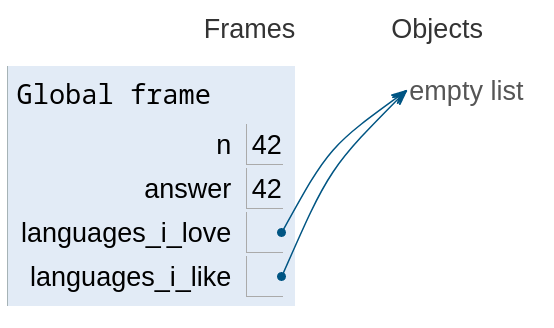
Valores de tipos imutáveis não mudam, então quando fazemos alguma
operação sobre eles (como somar 1) na verdade primeiro copiamos o
valor e então o modificamos. Operações sobre valores imutáveis inclui
o assignment, então ao fazermos answer = n, copia-se o valor de n
daquele momento para answer, e quaiquer modificações futuras de n
não se refletem de maneira alguma em answer.
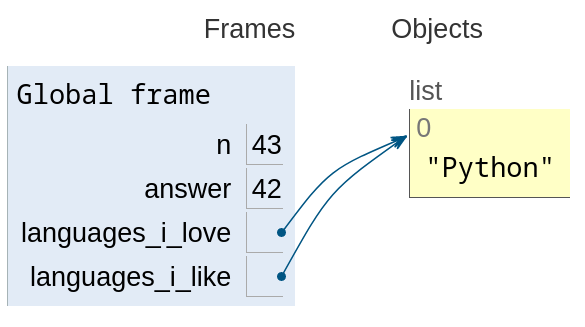
n = n + 1, languages_i_love.append("Python")) (visualização por Python Tutor)
No caso de valores de tipos mutáveis, ao fazermos languages_i_like =
languages_i_love, não há cópia alguma; é como se fossem nomes
diferentes para a mesma coisa. Quaisquer modificações da lista que é o
objeto a que os nomes se referem se refletem em ambos. Contudo, ao
fazer languages_i_like = languages_i_like + ["Dothraki"], como a
operação + em listas é pura, retornando uma nova lista, o assignment
quebra a ligação entre languages_i_love e languages_i_like: agora
uma se refere a uma lista e a outra se refere a uma outra lista, e
portanto modificações de uma lista não afetam a outra.
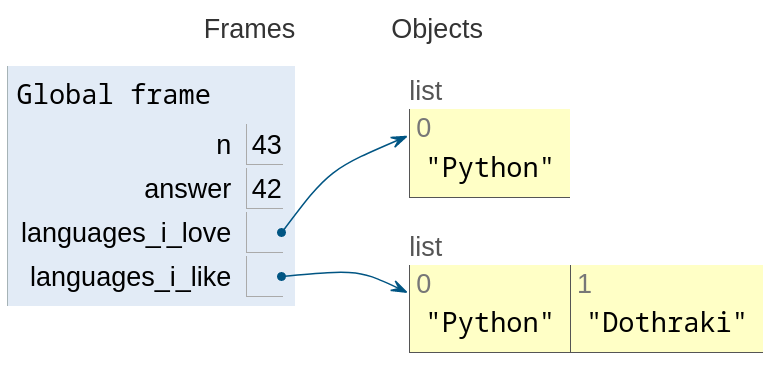
languages_i_like = languages_i_like + ["Dothraki"] (visualização por Python Tutor)6. Tuplas nomeadas
Tuplas são úteis para guardar informações, mas se tiverem muitos elementos seu uso começa a ficar desajeitado. É difícil de gravar a ordem correta dos elementos, e se trocarmos elementos de tipos iguais é difícil de perceber o erro.
# employee information is (name, age, title, department, paygrade) employee1 = ("Meredith Grey", 30, "Surgical resident", "Surgery", 110000.00) employee2 = ("Shonda Rhimes", 45, "Storyteller", "Well-Being", 200000.00)
Além disso, acessar os elementos também pode ser desajeitado, especialmente se não quisermos todos os valores de uma vez só.
drgrey = ("Meredith Grey", 30, "Surgical resident", "Surgery", 110000.00) name, age, jobtitle, department, paygrade = drgrey # ok jobtitle = drgrey[2] # não é muito informativo
Um grande problema é se decidirmos mudar o formato das tuplas. Digamos que queiramos incluir um novo elemento na tupla; se não colocarmos este elemento como último elemento da tupla, qualquer indexação anterior pode se tornar inválida:
# employee information now is (name, age, title, department, room_number, paygrade) drgrey = ("Meredith Grey", 30, "Surgical resident", "Surgery", "404A", 110000.00) drgrey[4] # era paygrade, agora é room_number
Da mesma forma, uma desestruturação da tupla antiga agora é inválida:
# ValueError: too many values to unpack (expected 5) name, age, jobtitle, department, paygrade = drgrey
Tudo isso indica que ao fazermos uma pequena modificação do nosso código (modificar o número de elementos de uma tupla) temos uma série de outras modificações em cascata que precisamos fazer para não criar bugs (em todo uso da tupla precisamos ajustar índices e desestruturação).
Felizmente, há uma forma melhor de usar tuplas para armazenar dados
estruturados: tuplas nomeadas. Cada tupla nomeada é na verdade um tipo
diferente, que precisamos criar com a função namedtuple. A função
retorna então um construtor, uma nova função que cria elementos do
tipo da tupla nomeada que acabamos de criar, e cujos argumentos são os
nomes que informamos como sendo os nomes da tupla nomeada. Veja o
exemplo:
from collections import namedtuple EmployeeRecord = namedtuple('EmployeeRecord', ['name', 'age', 'title', 'department', 'paygrade']) drgrey = EmployeeRecord(name="Meredith Grey", age=30, title="Surgical resident", department="Surgery", paygrade=110000) print(drgrey)
Nomear tuplas torna seu uso mais fácil, em parte porque temos uma
sintaxe especial para acessar suas componentes: ao invés de
drgrey[4] podemos fazer drgrey.paygrade. Outra facilidade é que se
adicionarmos um novo elemento nomeado à tupla, não precisamos de
modificar o código que usa os outros elementos, somente o que código
que cria tuplas.
EmployeeRecord = namedtuple('EmployeeRecord', ['name', 'age', 'title', 'department', 'room_number', 'paygrade']) drgrey = EmployeeRecord(name="Meredith Grey", age=30, title="Surgical resident", department="Surgery", paygrade=110000, room_number="404A") print(drgrey.name, drgrey.paygrade, drgrey.room_number)
6.1. Exercício: calculando saldo de transações
O aplicativo Tricount (e vários outros concorrentes) gerencia contas em grupo. Cada pessoa adiciona gastos compartilhados entre pessoas no grupo (por exemplo: pessoas em uma viagem, em que uma pagou o hotel, a outra alugou um veículo, outra contratou um guia), e no final o aplicativo calcula o quanto cada uma deve pagar ou receber para que todos fiquem quites.
Neste exercício, implemente uma das funcionalidades principais do
aplicativo: escreva a função calculate_balance, que dado o nome de
uma pessoa e uma lista de gastos, retorna o saldo da pessoa em relação
ao grupo. Se a pessoa pagou mais gastos do que ‘recebeu’ gastos de
outras pessoas, seu saldo é positivo, e caso contrário seu saldo é
negativo.
O nome das pessoas do grupo é sempre uma string, e o gasto será modelado como uma tupla nomeada:
Expense = namedtuple('Expense', ['name', 'payer', 'amount', 'beneficiaries']) example_expenses = [Expense(name="Breakfast", payer="Sam", amount=15.90, beneficiaries=["Frodo", "Sam", "Pippin"]), Expense(name="Breakfast (again)", payer="Pippin", amount=18.30, beneficiaries=["Frodo", "Sam", "Pippin"])]
em que name é um nome para o gasto (string), payer é o pagador
(string), amount é o valor que foi pago (float), e beneficiaries é
a lista dos nomes das pessoas por quem o gasto será dividido (lista de
strings).
Se você implementou calculate_balance corretamente,
calculate_balance("Frodo", example_expenses) deve retornar -11.4,
já que Frodo não pagou nada para ninguém e recebeu dois cafés da manhã
comprados por Sam e Pippin (nos valores totais de 15.90 e 18.30 cada,
divididos por três pessoas isso significa que Frodo deveria ter pago
11.40 se cada um tivesse pagado a sua parte de uma vez).