Capítulo 1 :
A Linguagem Scheme
Uma primeira visão que podemos ter de Scheme
é como uma calculadora:
escrevemos uma expressão e o interpretador Scheme nos
dá o resultado.
Portanto, nosso primeiro passo é ver como expressões
são escritas em Scheme.
1.1 : Notação Pré-fixada
A maneira de escrevermos expressões em Scheme é a primeira vista
um pouco estranha,
diferente da maneira como escrevemos expressões matemáticas.
Entretanto,
vamos perceber que a notação de Scheme tem uma grande vantagem,
que é a homogeneidade.
Existe basicamente uma única regra que rege a escrita de qualquer
expressão.
Em Scheme, quando queremos calcular o valor de uma função,
escrevemos (f x),
ao invés de f(x), como é usual em matemática.
Se a função tiver vários parâmetros, como g(x,y),
escrevemos
(g x y)
Os parênteses permitem o que chamamos de aninhamento
de expressões.
Assim, a expressão f(g(x)) é escrita como
(f (g x))
Os operadores aritméticos básicos (+, -, × , /),
apesar de usualmente escritos com notação infixada,
isto é, com o operador escrito entre os operandos, como em x + y,
na verdade são funções como outras quaisquer,
que têm como domínio os pares de reais e como imagem os reais.
Em Scheme, esses operadores são escritos como as outras funções,
no que é usualmente chamado de notação pré-fixada.
Então, 5 + 3 se escreve em Scheme como
(+ 5 3)
e (5+3) × 2 se escreve como
(* (+ 5 3) 2)
Observe que, no computador,
o operador de multiplicação × é usualmente escrito como *.
Exercício 1.1: Escreva as expressões abaixo na notação pré-fixada
de Scheme, e execute-as:
- 2+3
- 8/2
- 4
- 4.2 + 3.8
- 2 × 4+3
- 2+4 × 3
- (2+4) × 3
- 9 × (5-2)
- sin 3.1415
- 1+2+3
 1+2+3+4+5+6+7+8+9
1+2+3+4+5+6+7+8+9
- 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9
- (1+2+3+4+5) - 6
- (2+4) × (3+5)
- (9-5) × (8-3)
- (9/3) + (3*2)
 sin 4.5 + cos 3.7
sin 4.5 + cos 3.7
- log 4.5 + log 3.2
Exercício 1.2: Escreva as expressões abaixo em notação matemática usual:
-
(+ 3 2)
-
(- 9 5)
-
(+ 5 (/ 8 2))

(* 3.1 (+ 2 5.4))
-
(sin 3.14)
-
(* 2 -0.7 5)
-
(* (+ 3 4) 2)
-
(+ 4 (* 5 (/ 15 3)))
-
(+ (* (/ 15 3) 5) 4.5)
-
(* (+ 2 3) (+ 4 5))
-
(+ (/ 27 3) (* 3 2))
-
(* (+ 5 (+ 2 3)) 4)
-
(* (+ (+ 2 3) 4) (sin 5))
-
(/ (* (+ 8 a) (- b 4)) 2)
-
(/ (* (+ (- (+ 7 6) 5) 4) 3) 2)
-
(sin (* 2 x))

(+ (sin x) (cos x))

(sin (+ x (cos x)))
Por diversas razões,
é bastante comum em computação trabalharmos com números inteiros,
ao invés de números reais.
O conjunto de inteiros é fechado em relação às operações de
soma, subtração e multiplicação
(isto é, a soma, subtração e multiplicação de inteiros resultam
sempre em inteiros),
mas não em relação à divisão.
Por isso as vezes iremos usar dois outros operadores aritméticos:
um será escrito como a ÷ b,
que denota a parte inteira da divisão a/b;
o outro é escrito como a mod b,
denotando o resto da divisão de a por b.
Em geral, temos que
a = (a÷ b) × b + (a mod b)
Em Scheme, a ÷ b pode ser calculado com (quotient a b),
e a mod b com (remainder a b).
Exercício 1.3: Escreva as expressões abaixo na notação pré-fixada
de Scheme, e execute-as:
- 4 ÷ 2
- 5 ÷ 2
- 1 ÷ 2
- 1 mod 2
- 20 mod 3
 (5/2)-(5 ÷ 2)
(5/2)-(5 ÷ 2)
 (1345 ÷ 17) × 17 + (1345 mod 17)
(1345 ÷ 17) × 17 + (1345 mod 17)
1.2 : Um pouco de Sintaxe
Tudo que escrevemos em Scheme é chamado genericamente
de expressão S, ou mais simplesmente expressão.
As expressões que escrevemos em Scheme podem ser
classificadas em dois tipos:
átomos e listas.
Os átomos podem ser de três tipos (por enquanto):
numerais, por exemplo 4, -3.56;
textos (strings, em inglês),
que são sempre escritos entre aspas,
como "Um exemplo de texto";
e símbolos,
por exemplo a, define, nil?, +.
Uma lista, por sua vez, é uma sequência de expressões entre parênteses,
separadas por espaços;
por exemplo
(+ 3 4),
(define a (+ 3 x)),
(3 4 5),
(display "alo mundo") e
((3 4) (2 3) () ((9) +)).
Exercício 1.4: Quais dos exemplos a seguir não são expressões
sintaticamente corretas? Por quê?
-
(a b -
()
-
(((a)))
-
a b
-
(a b) c
-
(a b (c))
-
"(a b" -
a b)
-
(((a b) c) (d))
Na sintaxe de numerais,
vale a pena observar o uso do ponto decimal (como em inglês),
ao invés da vírgula,
e a possibilidade de usar notação científica
para números muito grandes ou muito pequenos.
Com essa notação, um valor como 3.5 × 10- 7
pode ser escrito como 3.5e-7.
Em geral,
espaços entre os diversos símbolos de uma expressão só são
relevantes para separar um símbolo de outro.
Assim, as expressões abaixo são equivalentes:
(a b (c))  ( a b ( c) )
( a b ( c) )
enquanto essas não são:
(a b (c)) 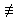 (ab (c))
(ab (c))
pois a b é interpretado como dois símbolos seguidos,
enquanto ab é considerado como um único símbolo.
Neste texto, apenas por convenção,
vamos usar apenas um único espaço entre duas expressões seguidas;
assim, escreveremos (a b (c d)),
e não ( a b( c d ) ).
Qualquer expressão pode ser quebrada em várias linhas;
para o interpretador,
uma mudança de linha equivale a um espaço em branco.
Em geral, o uso de quebras de linha pode ajudar na
leitura de expresões mais complexas.
Finalmente, podemos comentar expressões.
Por enquanto, como estamos usando a linguagem apenas
como uma calculadora, comentários não têm muita utilidade.
Mas mais adiante,
quando passarmos a definir funções mais complexas,
comentários passam a ser uma importante forma de colocarmos
explicações adicionais.
Um comentário é qualquer texto colocado em uma linha
após um ponto-e-vírgula (`;'),
e é totalmente ignorado pelo interpretador.
1.3 : Um pouco de Semântica
Cada uma das formas possíveis de expressões de Scheme tem um
valor associado;
geralmente, escrevemos uma expressão para que o intepretador
avalie esse valor.
Podemos representar o processo de cálculo que Scheme usa como
um processo de reescrita:
a cada passo da avaliação, uma parte da expressão é substituída
por seu valor, seguindo determinadas regras.
A medida que formos introduzindo novas construções em Scheme,
iremos definindo novas regras de como essas construções são reescritas.
Por enquanto, temos quatro regras,
uma para cada tipo de expressão:
-
Um numeral resulta no número correspondente.
Por exemplo, 4 resulta em 4.
-
Um texto resulta no próprio texto.
Por exemplo,
"Luiz Silva" resulta em "Luiz Silva".
-
Um símbolo resulta no valor associado a ele no ambiente,
através de um
define ou let
(que iremos tratar em breve).
-
O valor de uma lista já é um pouco mais complicado.
Primeiro calculamos o valor de cada elemento da lista.
O valor do primeiro elemento deve ser uma função,
que será aplicada aos outros valores.
A lista é então substituída (reescrita) pelo resultado
da função.
A sequência de substituições que uma lista sofre até chegar
ao seu valor final é chamada de traço.
Exemplo 1.1:
Vamos acompanhar os passos que Scheme dá para
calcular o valor da expressão abaixo:
(+ (* 8 -5) 7.3 (* 2 7.3))
(+ (* 8 -5) 7.3 (* 2 7.3))
 executa multiplicação
executa multiplicação
(+ -40 7.3 (* 2 7.3))
 executa multiplicação
executa multiplicação
(+ -40 7.3 14.6)
 executa soma
executa soma
-18.1  resultado final
resultado final
A cada passo, podemos colocar ao lado um pequeno texto
justificando aquele passo.
Em geral, essas explicações não são necessárias,
sendo usadas somente em situações mais complexas.
Da mesma forma, na medida em que ganhamos familiaridade
com a linguagem, passos intermediários podem ser pulados,
principalmente quando envolvem apenas operações aritméticas.
É importante ressaltar que, dada uma expressão,
não existe uma ordem fixa para seu traço.
Por exemplo, os dois passos abaixo são igualmente válidos:
(+ (* 8 -5) 7.3 (* 2 7.3))  (+ -40 7.3 (* 2 7.3))
(+ -40 7.3 (* 2 7.3))
(+ (* 8 -5) 7.3 (* 2 7.3))  (+ (* 8 -5) 7.3 14.6)
(+ (* 8 -5) 7.3 14.6)
Independentemente da ordem usada,
o resultado final será sempre o mesmo (por que?).
A regra de avaliação de listas acima
pode ser quebrada pelas chamadas formas especiais.
O exemplo mais característico de uma forma especial é o operador quote.
Esse operador tem a propriedade de não calcular seu único parâmetro.
Exercício 1.5: Experimente os exemplos abaixo:
-
(quote a)
-
(quote (+ 3 5))
-
(+ 3 5)
-
(quote (sin (+ 3.45 (* 5.65 23.4))))
-
(quote (mesa cadeira piso))
-
(quote 4.5)
Exercício 1.6: O operador quote é tão utilizado que existe uma
sintaxe especial para ele; experimente:
-
'a
-
'(a b c)
-
'(a 'b c)
-
'(a (b) (c d))
-
'(* (+ 3 2) (- 9 8))
1.4 : Definições
Uma primeira forma de abstração é darmos nomes às coisas.
Em Scheme, usamos o operador define para isso.
Por exemplo, (define x 3)
associa x ao valor 3.
Também podemos dizer que a variável x
tem valor 3.
A partir daí, quando calculamos o valor
da expressão x, o valor resultante será 3.
Como o valor definido pode ser usado em qualquer expressão
após a execução do define,
essas definições são chamadas de definições globais.
Exemplo 1.2:
Vamos acompanhar os passos que Scheme dá para
calcular o valor da expressão
(+ (* 8 b) a (* 2 a))
assumindo que a está definido como 7.3, e b como -5.
(+ (* 8 b) a (* 2 a))
 valor de
valor de b
(+ (* 8 -5) a (* 2 a))
 valor de
valor de a
(+ (* 8 -5) 7.3 (* 2 a))
 valor de
valor de a
(+ (* 8 -5) 7.3 (* 2 7.3))
 executa multiplicação
executa multiplicação
(+ -40 7.3 (* 2 7.3))
 executa multiplicação
executa multiplicação
(+ -40 7.3 14.6)
 executa soma
executa soma
-18.1  resultado final
resultado final
O conjunto de associações de nomes com valores
em vigor para uma determinada expressão é chamado de ambiente.
Neste texto, vamos usar a notação
{n1  v1,n2
v1,n2  v2,..., nn
v2,..., nn  vn}
para representar um ambiente onde o nome ni está
associado ao valor vi.
Por exemplo, após as definições
vn}
para representar um ambiente onde o nome ni está
associado ao valor vi.
Por exemplo, após as definições
(define aro 28)
(define arco (+ (* aro 3) 5))
teremos o ambiente global
{aro  28,
28, arco  89}.
Exercício 1.7: Qual o efeito das declarações abaixo, executadas em ordem?
89}.
Exercício 1.7: Qual o efeito das declarações abaixo, executadas em ordem?
-
(define pi 3.1415927)
-
(define raio 24.56)
-
(define area (* pi (* raio raio)))
-
(define nome "Maria Clara")

(define a +)
Uma outra forma de darmos nomes a valores é com
a construção let.
Essa construção
permite darmos nomes locais a valores.
Ao contrário de um define,
que define nomes globais,
esses nomes só são válidos dentro da
expressão onde eles são definidos,
não interferindo com outras partes de um programa.
A sintaxe geral de um let é:
(let ([nome1 exp1]
...
[nomen expn])
corpo)
observação: na construção acima,
e em algumas outras construções ao longo do texto,
iremos usar colchetes [...]
no lugar de parênteses (...),
de modo a deixar mais claro sua estrutura.
Entretanto, em qualquer uso real esses colchetes devem
ser substituídos por parênteses.
Quando executamos um let,
primeiro todas as expressões exp_i são calculadas,
e associadas aos respectivos nomes,
criando um ambiente local.
Em seguida, o corpo é calculado,
trocando-se cada ocorrência de
nome_i pelo valor correspondente no ambiente.
Exemplo 1.3: Para calcularmos o valor da expressão
(let ([x (+ 9 8)] ;lembre-se: trocar [...] por (...)
[y (sin 10)])
(+ (* x y) y))
executamos
(let ((x (+ 9 8)) (y (sin 10))) (+ (* x y) y))
 soma e seno
soma e seno
(let ((x 17) (y -0.544021)) (+ (* x y) y))
 corpo do
corpo do let
(+ (* x y) y)
{x 17,
17,y -0.544021}
-0.544021}
 ambiente local
ambiente local
(+ (* 17 -0.544021) -0.544021)
 aritmética
aritmética
-9.79238  resultado final
resultado final
A notação
(+ (* x y) y) {x 17,
17,y -0.544021}
-0.544021}
usada no traço acima,
significa que a expressão (+ (* x y) y) deve ser
executada no ambiente local
{x 17,
17,y -0.544021}.
-0.544021}.
É importante lembrar que as variáveis definidas em um let só
podem ser usadas no corpo do let;
em particular, uma variável não pode ser usada na definição
de outra variável, como na expressão abaixo:
; código incorreto!
(let ((x (sin 10))
(y (* x (+ x 10))))
(- x y))
Se necessário, tais situações podem ser tratadas com
lets aninhados, como no exemplo abaixo.
Exemplo 1.4: O corpo de um let pode conter outra expressão let,
como no caso abaixo:
(let ((x (sin 10)))
(let ((y (* x (+ x 10))))
(- x y)))
O traço dessa expressão segue a mesma regra do let:
(let ((x (sin 10))) (let ((y (* x (+ x 10)))) (- x y)))
 seno
seno
(let ((x -0.544)) (let ((y (* x (+ x 10)))) (- x y)))
 corpo
do 1o
corpo
do 1o let
(let ((y (* x (+ x 10)))) (- x y)) {x -0.544}
-0.544}
 valor
de
valor
de x
(let ((y (* -0.544 (+ -0.544 10)))) (- -0.544 y))
 aritmética
aritmética
(let ((y -5.14425)) (- -0.544 y))
 corpo do
corpo do let
(- -0.544 y) {y -5.14425}
-5.14425}
 valor de
valor de y
(- -0.544 -5.14425)
 aritmética
aritmética
4.60023 
Os principais usos da construção let são
na simplificação de expressões muito complexas e
para colocar em evidência sub-expressões comuns.
Por exemplo, considere a expressão
(- (sin (+ a (* b c))) (cos (+ a (* b c))))
Com esse código, não só escrevemos duas vezes a
sub-expressão (+ a (* b c)),
como fazemos o computador calculá-la duas vezes.
Se reescrevermos a expressão como
(let ((x (+ a (* b c)))) (- (sin x) (cos x)))
eliminamos os dois problemas.
Exercício 1.8: Calcule o valor das expressões abaixo:1
-
(let ((x 10) (y 5)) (* (+ x y) (- x y)))
-
(let ((x (sin 5))) (* x x))
-
(+ 10 (let ((x (sin 5))) (* x x)))
-
(let ((x 10)) (let ((y (+ x 5))) (* x y)))
-
(let ((delta (- (* b b) (* 4 a c)))
(dois-a (* 2 a)))
(/ (+ (- b) (sqrt delta)) dois-a))
assumindo que a, b e c estejam definidos como
-1, 1 e 2 respectivamente.
Observe como, em todas essas expressões,
os nomes x, y, etc não precisavam estar definidos previamente;
por outro lado,
no caso de haver um define prévio de qualquer desses nomes,
após a expressão o nome continua
representando o valor que representava antes,
pois um nome definido por um let só é válido
dentro do corpo do let.
Exercício 1.9: Primeiro, defina globalmente (com defines)
o ambiente {x 5,
5, y 10}.
Em seguida, calcule o valor das expressões abaixo:
10}.
Em seguida, calcule o valor das expressões abaixo:
-
(+ x (let ((x (sin 5))) (* x x)))
-
(- (let ((x (sin 5))) (* x y)) x)
1.5 : Listas
Muitas vezes precisamos trabalhar com um conjunto de dados com
alguma estrutura.
Exemplos típicos são matrizes de números
ou conjuntos.
Uma linguagem de programação deve oferecer formas de
estruturarmos os dados básicos (como números),
que nos permitam criar dados mais complexos.
Em Scheme, o mecanismo básico de estruturação de dados é a lista.
Já vimos listas anteriormente, quando vimos a sintaxe de Scheme;
agora vamos ver como podemos manipular listas em um programa.
Listas representam sequências de valores.
Como listas também são valores, podemos ter listas como
elementos de outras listas;
essas listas são chamadas aninhadas.
É importante perceber o significado de aninhamentos;
por exemplo, a lista (10 20 40) tem 3 elementos, 10, 20 e 40,
enquanto a lista ((10 20 40)) tem apenas 1 elemento,
que é a lista (10 20 40).
Uma primeira forma de criarmos listas é com o operador quote,
que também já vimos anteriormente.
Outra forma é com a função (cons a b),
que acrescenta o elemento a no início da lista b.
Por exemplo,
(cons 3 '(4 5))  (3 4 5)
(3 4 5)
Vale a pena ressaltar que cons sempre precisa de uma lista
como seu segundo argumento.2
Portanto, para criarmos uma lista com
um único elemento x, devemos escrever (cons x '()),
colocando esse elemento no início de uma lista vazia;
e para criarmos uma lista com dois elementos x e y,
devemos escrever (cons x (cons y '())),
e não (cons x y).
Em geral, qualquer lista pode ser construída por sucessivas
aplicações de cons sobre a lista vazia.
Por exemplo, a lista (4 10 23 1) pode ser criada pela
expressão
(cons 4 (cons 10 (cons 23 (cons 1 '()))))
Igualmente, listas aninhadas
também podem ser construídas somente com cons.
Por exemplo,
(cons (cons 4 (cons 5 '())) (cons 2 '()))  ((4 5) 2)
((4 5) 2)
Quando queremos escrever uma lista diretamente,
com valores fixos, é mais conveniente usarmos quote.
Assim, uma lista como (4 10 23 1) pode ser escrita
diretamente em Scheme precedida pelo quote: '(4 10 23 1).
Note, entretanto, que o quote só serve para construirmos listas
com valores constantes.
Exercício 1.10: Qual o valor das expressões abaixo?
-
(cons 2 '())
-
(cons 1 (cons 2 '()))
-
(cons 1 (cons 2 (cons 3 '())))
-
(cons 'China '(Uruguai Grecia))
-
(cons '() '())
-
(cons '() '(a b c))
-
(cons '(a b c) '(d))
-
(let ((x 'Paris) (y '(Roma Berlin))) (cons x y))
-
(let ((x 'Paris) (y '(Roma Berlin))) (cons 'x y))
-
(let ((n '())) (cons (cons 3 n) n))
-
(cons 2 (let ((x '())) (cons x x)))
-
(let ((x '(y z))) (cons 'x x))
Exercício 1.11: Usando apenas números, cons e a lista vazia,
escreva expressões que resultem nas listas abaixo:
-
(2 4)
-
((2 4))
-
(((2 4)))
-
((2 4) (3 5))
Para `desmontarmos' uma lista,
temos duas funções, que fazem o inverso de cons:
car e cdr.
car retorna o primeiro elemento de uma lista,
enquanto cdr retorna o resto da lista, isto é,
a lista sem o seu primeiro elemento.
Por exemplo, se definirmos l como sendo a lista
(a b c), então (car l) será a
e (cdr l) será (b c).
Em geral, se b é uma lista qualquer, temos que
(car (cons a b))  a
a
(cdr (cons a b))  b
b
Note que o cdr de uma lista é sempre uma lista.
Se x é uma lista não vazia,
temos também que
(cons (car x) (cdr x))  x
x
Exercício 1.12: Qual o valor das expressões abaixo?
-
(car '(a b))
-
(cdr '(a b))
-
(car '(a))
-
(car '((a)))
-
(cdr '(a))
-
(cdr '((a)))
-
(let ((l '(lua sol marte))) (cdr l))
-
(let ((l '(lua sol marte))) (car (cdr l)))
-
(let ((l '(lua sol marte))) (car (cdr (cdr l))))
-
(let ((lista '((a1 b1) (a2 b2) (a3 b3)))) (car (cdr (car lista))))
Apesar de car só acessar o primeiro elemento de uma lista,
combinando aplicações de car e cdr
podemos acessar qualquer parte de uma dada lista.
Por exemplo, o segundo elemento de uma lista l
pode ser acessado com a expressão (car (cdr l)).
Para simplificar essas composições,
Scheme oferece algumas formas compactas,
como exemplificado abaixo: (car (cdr l))  (cadr l)
(cadr l)
(car (car l))  (caar l)
(caar l)
(cdr (car l))  (cdar l)
(cdar l)
((car (car (car l))))  (caaar l)
(caaar l)
Essas formas compactas existem para qualquer combinação de até quatro
níveis de car com cdr.
Exercício 1.13: Defina l como sendo a lista ((a b c) (e f) g).
Diga qual forma compacta deve ser usada para:
 extrair
extrair a de l;
- extrair
b de l;
- extrair
c de l;
- extrair
e de l;
 extrair
extrair f de l;
- extrair
g de l.
1.6 : Definindo Funções
Uma segunda forma de abstração,
bem mais poderosa que o uso de nomes,
é a definição de funções.
Em matemática,
escrevemos f(x) = 2x para definir uma função f
que leva um número ao seu dobro.
Em Scheme, essa função seria definida como:
(define f (lambda (x) (* 2 x)))
A construção lambda usada acima serve
exatamente para criarmos funções.
O construtor lambda atua sobre
uma lista com os parâmetros da função
e um corpo que calcula o valor da função.
No nosso exemplo, o único parâmetro é x,
e o corpo é a expressão (* 2 x).
O define é usado como sempre,
para dar um nome à função criada com o lambda.3
Uma vez definida, uma função pode ser usada como qualquer outra em Scheme,
bastando escrever uma lista com seu nome seguido dos eventuais argumentos;
após definir f como acima,
experimente executar (f 3).
De maneira geral, sempre que escrevemos uma nova função devemos
testá-la, isto é,
aplicá-la sobre alguns valores para verificar se ela está correta.
Funções podem ter zero, um, ou mais parâmetros.
Por exemplo, uma função para tirar a média entre três números
pode ser escrita como
(define media (lambda (x y z) (/ (+ x y z) 3)))
e usada, por exemplo, na expressão (media 5.7 6.3 8.1).
Como terminologia, dizemos que chamamos a função media
passando como parâmetros os valores 5.7, 6.3 e 8.1;
a função media, quando chamada, recebe esses valores
e retorna um resultado.
Exercício 1.14: Defina (e teste) as seguintes funções em Scheme:
 dobro(x) = 2x
dobro(x) = 2x
- quadrado(x) = x2
- incrementa(x) = x+1
- decrementa(x) = x-1
- f(x,y) = x+y (adição)
- f(x) = 3 (função constante)
 f(x,y) = 10 (função constante com dois parâmetros)
f(x,y) = 10 (função constante com dois parâmetros)
- uma função que retorne a área da circunferência para um dado raio;
- uma função que retorne o perímetro da circunferência para um dado raio;
- f(x,y) = 2x + 5y
 f(x,y,z) = 10x + 5y - z
f(x,y,z) = 10x + 5y - z
- f(x) = (sin x)2 + (cos x)2
-
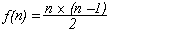
 uma função que retorne o segundo elemento de uma dada lista;
uma função que retorne o segundo elemento de uma dada lista;
- uma função que retorne o terceiro elemento de uma dada lista;
- uma função que receba uma lista de números e retorne a soma
do primeiro com o segundo elemento;
- uma função que receba dois valores e retorne uma
lista com esses valores;
- uma função que calcule a raiz de uma equação de 2o grau:
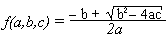 (dica: use
(dica: use let para calcular o valor intermediário
delta = b2 - 4ac.)
Assim como em matemática,
cada função em Scheme é limitada a um determinado domínio;
não podemos aplicar qualquer função a qualquer valor.
Por exemplo, chamadas como (sin '(a b)) ou (car 4),
se executadas, irão resultar em situações de erro.
Da mesma forma, as funções em Scheme tem um contra-domínio,
que é o conjunto de valores que a função pode retornar.
Por exemplo, o contra-domínio da função cons é o conjunto
de todas as listas.
As condições que os argumentos de uma função têm que satisfazer
para que a função opere corretamente são chamadas de
pré-condições da função.
Por exemplo, a pré-condição de (sin x) é que x seja um
número real, ou seja, x 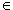
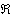 .
Já a pré-condição da função dada no exercício 1.14.n é
que seu argumento seja uma lista com comprimento maior ou igual a 2;
de outra forma, não podemos retornar seu segundo elemento.
Muitas vezes, não explicitamos as pré-condições de uma função.
No entanto, é muito importante que sempre tenhamos conciência do
domínio de validade de qualquer função que usamos.
Muitos erros em programas são causados por funções sendo chamadas
com argumentos inválidos ou não previstos.
Exercício 1.15: Descreva as pré-condições de cada uma das funções definidas
no exercício anterior.
Descreva também os domínios e contra-domínios dessas funções.
Conforme explicado acima,
o
.
Já a pré-condição da função dada no exercício 1.14.n é
que seu argumento seja uma lista com comprimento maior ou igual a 2;
de outra forma, não podemos retornar seu segundo elemento.
Muitas vezes, não explicitamos as pré-condições de uma função.
No entanto, é muito importante que sempre tenhamos conciência do
domínio de validade de qualquer função que usamos.
Muitos erros em programas são causados por funções sendo chamadas
com argumentos inválidos ou não previstos.
Exercício 1.15: Descreva as pré-condições de cada uma das funções definidas
no exercício anterior.
Descreva também os domínios e contra-domínios dessas funções.
Conforme explicado acima,
o define e o lambda tem significados
independentes, e são muitas vezes usados separadamente.
O lambda cria funções,
enquanto o define nomeia valores
que, em particular, podem ter sido criados
por uma expressão lambda.
Por outro lado, é extremamente comum usarmos a
combinação
(define f
(lambda (x y)
... ))
Nesses casos, podemos reescrever a definição da função como
(define (f x y)
... )
É importante frizarmos que essa segunda forma tem exatamente o mesmo
significado da primeira,
sendo apenas uma maneira mais compacta de escrevermos uma mesma coisa.
De forma a deixar mais claro o papel de cada construção,
neste texto vamos procurar usar a notação básica,
escrevendo o lambda explicitamente.
1.7 : Semântica de Funções
Quando reescrevemos uma expressão,
o que ocorre com uma função?
Por exemplo,
se tivermos uma definição como
(define media (lambda (x y) (/ (+ x y) 2)))
como fazer o traço da expressão (media (* 8 9) 3)?
Primeiro, podemos seguir as regras normais:
(media (* 8 9) 3)
 multiplicação
multiplicação
(media 72 3)
 valor de
valor de media
((lambda (x y) (/ (+ x y) 2)) 72 3) 
Note como substituimos media por seu valor,
como fazemos com qualquer símbolo.
Em seguida, aplicamos uma nova regra:
uma lista cujo primeiro valor seja
uma expressão lambda pode ser substituída
pelo corpo da expressão lambda;
no exemplo acima, o corpo da função é (/ (+ x y) 2).
Esse corpo terá como ambiente local a associação dos
argumentos com os parâmetros correspondentes;
no nosso exemplo,
os parâmetros são x e y,
e os argumentos são 72 e 3,
resultando no ambiente {x 72,
72, y 3}.
Aplicando a regra toda, temos:
3}.
Aplicando a regra toda, temos:
((lambda (x y) (/ (+ x y) 2)) 72 3)
 corpo do lambda
corpo do lambda
(/ (+ x y) 2) {x 72,
72, y 3}
3}
 valores
de
valores
de x e y
(/ (+ 72 3) 2)
 aritmética
aritmética
37.5  resultado final
resultado final
Vale a pena observar que existe uma similaridade entre
as construções lambda e let.
Ambas avaliam seu corpo substituindo nele nomes locais
por seus valores.
Entretanto,
no let esses valores são definidos na própria
expressão,
enquanto no lambda os valores dos nomes locais
só são definidos quando a função é chamada.
Em geral, qualquer let poderia ser reescrito segundo
a regra abaixo:
(let ([n1 e1] ... [nn en]) corpo)  ((lambda (n1 ... nn) corpo) e1 ... en)
((lambda (n1 ... nn) corpo) e1 ... en)
Exercício 1.16: Escreva os traços das expressões abaixo:
-
((lambda (x y) 10) 3 (* 8 3))
-
((lambda (x y) (let ((z x)) (+ z y))) 15 23)
-
((lambda (x) (* x x)) (let ((x 2)) (+ x 4)))


(((lambda (x) (lambda (y) (- x y))) 4) 5)
As regras colocadas acima para traços de chamadas de
funções devem ser usadas apenas quando estamos interessados
no funcionamento da função,
por exemplo quando estamos
testando se ela funciona corretamente.
Uma vez que uma função esteja definida corretamente,
e tenhamos entendido bem o que ela faz,
podemos passar da sua chamada ao resultado
final em apenas um passo.
Quando usamos a função media
em outras expressões mais complexas,
podemos em um único passo substituir a sub-expressão
(media x y) pela média aritmética de x e y.
Na realidade, já fazíamos isso com outras funções:
quando escrevemos algo como (sin x),
existe em algum lugar da máquina uma definição de como
se calcula um seno.
Mas para nós a chamada é abstrata,
e substituimos direto (sin x) pelo seno de x.
Essa é a grande capacidade de abstração que funções
proporcionam:
uma vez (corretamente) definida,
podemos usar qualquer função da mesma forma que qualquer
outra operação da nossa linguagem,
sem nos preocuparmos em como ela foi escrita e/ou
como funciona.
Vale a pena lembrarmos que tal raciocínio abstrato só
é válido quando a função está definida corretamente.
Caso contrário, esse raciocínio pode nos criar enormes
dificuldades de entendimento;
imagine você tentando saber por que uma
fórmula está dando um valor incorreto,
quando a função sin que você está usando é que
está retornando um valor errado.
Por isso, é extremamente importante que toda nova função,
uma vez definida, seja testada adequadamente,
para podermos ter alguma confiança na sua corretude.
Nunca é demais enfatizar a importância de mecanismos de
abstração:
eles formam a essência do poder de um computador.
Saber programar significa saber explorar esses mecanismos,
por exemplo
definindo novas funções de forma a estender a capacidade
de uma linguagem ou de um programa.
Não só linguagens de programação oferecem esses mecanismos:
até mesmo editores de texto possibilitam a criação de
abstrações úteis.
Saber explorar esses mecanismos é o que distingue um
expert de um usuário medíocre.
1.8 : Predicados
Existe uma classe de funções em matemática que retornam como valor
simplesmente verdadeiro ou falso,
isto é, tais funções apenas
testam uma determinada propriedade.
Exemplos comuns são os operadores de comparação,
como x 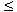 y e x
y e x  y, e pertinência em conjuntos (x
y, e pertinência em conjuntos (x 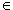 Y).
Chamamos esse tipo de função de predicado.
Predicados em Scheme são escritos como qualquer outra função,
mas retornam valores especiais que representam
verdadeiro ou falso.
Em Scheme, o valor verdadeiro é denotado pelo símbolo
Y).
Chamamos esse tipo de função de predicado.
Predicados em Scheme são escritos como qualquer outra função,
mas retornam valores especiais que representam
verdadeiro ou falso.
Em Scheme, o valor verdadeiro é denotado pelo símbolo #t,
e o valor falso pelo símbolo #f.4
Em outras palavras, predicados são funções cujo contra-domínio
é o conjunto {#f, #t}.
A comparação x<y pode ser escrita em Scheme como (< x y).
Nessa expressão, < é uma função que retorna #t ou #f,
dependendo se x é ou não menor que y.
Como o teclado normal de um computador não possui o símbolo 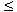 ,
este é escrito como
,
este é escrito como <=.
Assim, x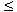 y vira
y vira (<= x y).
Da mesma forma, o predicado  é escrito como
é escrito como >=.
Muitas linguagens de programação usam essa mesma sintaxe
para esses operadores.
Existem diversos predicados que operam sobre
átomos e listas em geral.
De especial importância para nós é o predicado
null?, que testa se uma lista é vazia.
Note que, por convenção, nomes de predicados costumam terminar
com um ponto de interrogação.
Outros predicados bastante úteis são os de igualdade.
Para compararmos se dois números são iguais,
usamos o predicado =;
para outros tipos de átomos, usamos o predicado equal?.
Exercício 1.17: Qual o valor das expressões abaixo?
-
(null? '(a))
-
(null? '())
-
(null? '(()))
-
(let ((l '(()))) (null? (car l)))
-
(let ((x (* 8 5))) (= x 40))
-
(let ((x 'abobora)) (equal? x 'abobora))
-
((lambda (x) (equal? x "Jose")) "Jose")
-
((lambda (x y) (= x y)) 1 1.0)
Scheme define vários outros predicados úteis.
Ao longo do texto, vamos usar alguns deles:
-
number? Testa se um dado valor é um número.
-
symbol? Testa se um dado valor é um símbolo.
-
list? Testa se um dado valor é uma lista.
-
even? Testa se um dado número inteiro é par.
-
odd? Testa se um dado número inteiro é ímpar.
-
positive? Testa se um dado número é maior que 0.
-
zero? Testa se um dado número é igual a 0.
Como predicados são funções,
podemos definir novos predicados da mesma
forma que definimos funções,
com o construtor lambda.
Exemplo 1.5: O predicado zero?, se não fosse pré-definido,
poderia ser escrito como
(define zero? (lambda (x) (= x 0)))
Exemplo 1.6: O predicado abaixo testa se um número é divisível por outro,
verificando se o resto da divisão de um pelo outro é zero:
(define divide?
(lambda (x y)
(zero? (remainder x y))))
Exercício 1.18: Defina os seguintes predicados em Scheme:
- um predicado para verificar se um número é múltiplo de 3;
 um predicado para verificar se um número é maior que 5;
um predicado para verificar se um número é maior que 5;
- um predicado para verificar se um número é maior ou igual a 5;
- um predicado para verificar se um número não é maior ou igual a 5;
 um predicado para verificar se um número é
menor que
um predicado para verificar se um número é
menor que 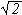 .
.
1.9 : Condicionais
Muitas vezes, precisamos descrever uma função por casos.
Um exemplo tradicional é a função de valor absoluto,
em que f(x) é x se x  0, e -x caso contrário.
Traduzindo a expressão acima para Scheme, teremos:
0, e -x caso contrário.
Traduzindo a expressão acima para Scheme, teremos:
(define f
(lambda (x)
(if (>= x 0) x (- x))))
O if é um operador que recebe três argumentos;
dependendo do primeiro argumento ser verdadeiro ou falso,
ele escolhe seu valor entre o segundo e o terceiro.
No exemplo acima, se (>= x 0) for verdadeiro,
o valor do if será o valor de x;
caso contrário, o valor do if será o valor de (- x).
A semântica do if pode ser dada pelas suas
regras de reescrita:
(if '#t b c)  b
b
(if '#f b c)  c
c
Note que só podemos reescrever um if após termos
calculado sua condição.
Quando precisamos testar entre mais de dois casos,
usamos o que se chama aninhamento de ifs:
um dos casos do if (ou os dois) é um outro if.
Exemplo 1.7: A função abaixo retorna o sinal de um número:
-1 se ele é negativo, 0 se ele é 0, e +1 se ele é positivo:
(define sig
(lambda (x)
(if (< x 0)
-1
(if (> x 0) 1 0))))
O traço da chamada (sig 3) pode ser escrito como abaixo:
(sig 3)
 definição de
definição de sig
((lambda (x) (if (< x 0) -1 (if (> x 0) 1 0))) 3)
 lambda, com
{
lambda, com
{x 3}
3}
(if (< 3 0) -1 (if (> 3 0) 1 0))
 comparação
comparação
(if '#f -1 (if (> 3 0) 1 0))
 regra do
regra do if
(if (> 3 0) 1 0)
 comparação
comparação
(if '#t 1 0)
 regra do
regra do if
1 
Exercício 1.19: Defina e teste as seguintes funções em Scheme.
Teste cada função com diversos valores,
correspondentes aos diversos casos:
-
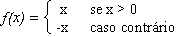
-
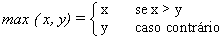
-
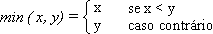
-
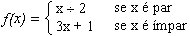
-
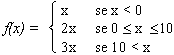
-
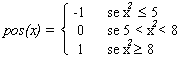 (dica: use
(dica: use let para calcular x2 uma única vez.)
Outra construção para expressões condicionais é o cond,
que é uma espécie de generalização do if para vários casos.
A forma geral do cond é
(cond [c1 e1]
[c2 e2]
...
[cn en]
[else e])
observação: novamente
usamos colchetes [...]
no lugar de parênteses (...),
de modo a deixar mais claro o formato do cond.
Novamente, em qualquer uso real esses colchetes devem
ser substituídos por parênteses.
Exemplo 1.8: A função sig, definida no exemplo 1.7,
poderia ser redefinida com cond, conforme mostrado abaixo:
(define sig
(lambda (x)
(cond
[(< x 0) -1] ;lembre-se: trocar [...] por (...)
[(> x 0) 1]
[else 0])))
A semântica do cond pode ser dada pelas regras:
(cond ('#t e) ...)  e
e
(cond ('#f e) (c e') ...)  (cond (c e') ...)
(cond (c e') ...)
(cond (else e))  e
e
Isso é, calculamos a primeira condição;
se seu valor for verdadeiro,
o valor do cond será o valor da expressão correspondente.
Caso seu valor seja falso,
a opção é descartada e passamos para a opção seguinte.
Caso nenhuma das condições seja verdadeira,
todas serão descartadas e a última expressão,
associada ao símbolo else, será usada.
As construções if e cond são de certo
modo equivalentes,
e tudo que pode ser escrito com uma pode ser escrito com a outra:
(if a b c)  (cond (a b) (else c))
(cond (a b) (else c))
(cond (c1 v1) (c2 v2) (else v))  (if c1 v1 (if c2 v2 v))
(if c1 v1 (if c2 v2 v))
Para verificarmos a primeira equivalência,
basta vermos que ambas as expressões são sempre reduzidas
para o mesmo resultado.
Quando a for falso, temos pela regra do if que:
(if '#f b c)  c
c
Por outro lado, usando as regras do cond, temos:
(cond ('#f b) (else c))  (cond (else c))
(cond (else c))  c
c
Quando a é verdadeiro, temos:
(if '#t b c)  b
b
(cond ('#t b) (else c))  b
b
A segunda equivalência pode ser mostrada de maneira semelhante.
Neste texto,
vamos procurar usar if sempre que tivermos apenas dois casos,
e cond nas outras situações.
Lembre-se que qualquer função pode ser escrita de diversas maneiras.
As vezes, uma maneira pode ser `melhor',
ou por ser mais simples, ou mais fácil de entender,
ou mais eficiente.
Outras vezes, a escolha é apenas uma questão de gosto e hábito.
Exercício 1.20: Reescreva as funções do exercício 1.19 usando cond
no lugar de if.
Para juntarmos dois ou mais testes,
usamos os chamados operadores lógicos.
Por exemplo, o teste i < j < l tem na verdade duas comparações,
de i com j e de j com l.
Estamos testando se ambas são verdadeiras,
então unimos os testes com um and (`e' em inglês).
Ou seja, o teste seria (i < j) e (j < l).
Na notação pré-fixada,
(and (< i j) (< j l)).
As regras de reescrita para o and são:
(and #f a)  #f
#f
(and #t a)  a
a
Da mesma forma que o and testa se duas (ou mais) condições são
simultaneamente verdadeiras,
o or (`ou' em inglês) testa se alguma condição é verdadeira.
Assim, o teste
(or (< i j) (> i k))
verifica se i é menor que j ou maior que k.
As regras de reescrita para o or são:
(or #f a)  a
a
(or #t a)  #t
#t
Finalmente, existe o operador not (`não'),
que inverte o resultado de um teste.
Por exemplo,
(not (< i j)) é equivalente a (>= i j),
enquanto (not (= i j))
testa se i e j são números diferentes.
Note que, em geral, se a e b são duas expressões quaisquer,
temos que:
(and a b)  (if a b #f)
(if a b #f)
(or a b)  (if a #t b)
(if a #t b)
(not a)  (if a #f #t)
(if a #f #t)
ou seja, todos esses operadores lógicos podem ser
substituídos pelo if.
Usualmente, essas equivalências são usadas na outra direção,
substituindo-se ifs por operadores lógicos,
por resultar em expressões mais simples.
Temos também que:
(if (not a) b c)  (if a c b)
(if a c b)
isto é, sempre podemos trocar a ordem dos casos em
um if negando sua condição.
De modo geral, costumamos tratar primeiro o caso
mais simples.
Exercício 1.21: Escreva em Scheme os predicados (funções) para
as propriedades abaixo, e teste-os.
Não use if nem cond.
- número está no intervalo [3, 50];
- número está no intervalo [3,30);
- número está fora do intervalo [3,30);
- número é par maior que 10;
- número é impar entre 5 e 15;
 lista tem pelo menos dois elementos;
lista tem pelo menos dois elementos;
- os dois primeiros elementos de uma dada lista são iguais.
Exercício 1.22: Reescreva os predicados do exercício anterior sem
usar and, or, ou not.
Troque-os por ifs ou conds.
Exercício 1.23:  Reescreva os predicados abaixo,
sem usar o operador
Reescreva os predicados abaixo,
sem usar o operador not:
-
(not (< x 0))
-
(not (>= x y))

(not (and (> x 5) (<= x 10)))
-
(not (or (<= x 5) (> x 10)))

Figura 1.1: Tabela (fictícia) de imposto de renda devido.
Exercício 1.24: Escreva uma função que,
dado o total dos rendimentos tributáveis de uma pessoa,
retorne o valor do imposto devido.
Baseie sua função na tabela fictícia mostrada na figura 1.1.
Por exemplo, o imposto devido por alguém que teve um total anual
de rendimentos tributáveis igual a R$53.200
será igual a
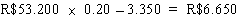 .
.
Capítulo 2 :
Recursão
Até agora,
vimos como definir funções compondo outras funções já existentes,
e/ou definindo casos, com ifs e conds.
Com esse arsenal de mecanismos,
ficamos muito dependentes de que funções o sistema nos oferece,
pois nosso poder para criar novas funções ainda é muito pequeno.
Como exemplo padrão,
considere a função fatorial:
n! = n × (n-1) × ... × 1
Apesar da nossa linguagem ter um operador de multiplicação,
não temos como expressar uma multiplicação
envolvendo um número variável de fatores.
Como podemos definir uma função como essa?
Uma primeira forma seria termos a função fatorial pré-definida
na nossa linguagem (como temos seno, cosseno, etc).
Isso aumentaria o tamanho e a complexidade da linguagem,
sem efetivamente resolver nosso problema,
pois nenhuma linguagem pode implementar todas as funções
que todos poderão precisar.
Uma outra solução é encontrar algum mecanismo que nos permita
expressar a função fatorial,
e muitas outras funções úteis.
Um mecanismo bastante poderoso
(em um certo sentido, `o mais poderoso')
para criarmos novas funções é a recursão.
Dizemos que uma definição é recursiva quando usamos
o próprio termo sendo definido dentro da definição.
Esse ciclo na definição pode nos levar a definições sem
sentido, como por exemplo f(x)=f(x);
tal `definição' não nos diz nada sobre a função f.
Mas em outros casos,
é exatamente da natureza cíclica de uma definição recursiva
que vem seu poder de expressão.
Voltemos ao exemplo da função fatorial.
Uma outra forma de definirmos essa função,
sem usarmos ` ... ',
é mostrada abaixo:
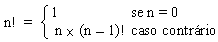 Note que usamos a própria função sendo definida na sua definição,
caracterizando uma definição recursiva.
A definição acima pode ser diretamente traduzida para
a notação pré-fixada:
Note que usamos a própria função sendo definida na sua definição,
caracterizando uma definição recursiva.
A definição acima pode ser diretamente traduzida para
a notação pré-fixada:
(define fat
(lambda (n)
(if (zero? n)
1
(* n (fat (- n 1))))))
Em geral, uma definição recursiva é definida por casos:
um caso base, e um caso recursivo.
O caso base é geralmente uma situação trivial
(número 0, lista vazia, etc), onde calcular o valor
da função também é trivial, e não envolve recursão.
No exemplo acima, o caso base é 0!=1.
No caso recursivo, por sua vez,
é fundamental que façamos a aplicação recursiva sobre
uma situação `mais simples' que a original, isto é,
mais próxima do caso base.
No nosso exemplo, se queremos n!, calculamos (n-1)!
(observe que n-1 está mais próximo de 0 do que n).
Sabendo o resultado dessa aplicação recursiva,
precisamos então descobrir como modificar esse resultado
para termos o resultado que procuramos.
No exemplo acima, basta multiplicarmos (n-1)! por n.
Uma boa maneira de melhorarmos nossa compreensão sobre o
funcionamento de uma função recursiva
(e acreditar que não temos um círculo vicioso)
é fazendo o traço de sua execução.
O traço de uma função recursiva é feito da mesma forma que o de
uma função não recursiva.
Em particular, tratamos a chamada recursiva exatamente como
trataríamos uma chamada a uma outra função.
Por exemplo,
o traço da chamada (fat 4) será:
(fat 4)
 corpo de fat
corpo de fat
(if (zero? 4) 1 (* 4 (fat (- 4 1))))
 condicional
condicional
(* 4 (fat 3))
 corpo de
corpo de fat
(* 4 (if (zero? 3) 1 (* 3 (fat (- 3 1)))))
 condicional
condicional
(* 4 (* 3 (fat 2)))
 corpo de
corpo de fat
(* 4 (* 3 (if (zero? 2) 1 (* 2 (fat (- 2 1))))))
 condicional
condicional
(* 4 (* 3 (* 2 (fat 1))))
 corpo de
corpo de fat
(* 4 (* 3 (* 2 (if (zero? 1) 1 (* 1 (fat (- 1 1)))))))
 condicional
condicional
(* 4 (* 3 (* 2 (* 1 (fat 0)))))
 corpo de
corpo de fat
(* 4 (* 3 (* 2 (* 1 (if (zero? 0) 1 (* 0 (fat (- 0 1))))))))
 caso base
caso base
(* 4 (* 3 (* 2 (* 1 1))))
 multiplicação
multiplicação
(* 4 (* 3 (* 2 1)))
 multiplicação
multiplicação
(* 4 (* 3 2))
 multiplicação
multiplicação
(* 4 6)
 multiplicação
multiplicação
24  resultado final
resultado final
Observe como a chamada recursiva vai se `desenrolando' repetidamente,
até chegar no caso base.
A partir daí, vai `retornando' e executando as operações
que ficaram pendentes (no caso acima, as multiplicações).
Um outro exemplo clássico é uma função que calcula o comprimento
de uma dada lista.5
Essa função tem como domínio o conjunto de listas e como
contra-domínio os números naturais:
(define comp
(lambda (l)
(if (null? l)
0
(+ 1 (comp (cdr l))))))
Nesse exemplo, o caso base é sobre a lista vazia,
cujo comprimento é 0.
A chamada recursiva, por sua vez,
é feita sobre o cdr da lista original,
que é uma lista `mais próxima' da lista vazia.
Neste caso, o comprimento da lista é simplesmente 1 a mais
que o comprimento do seu cdr.
O traço da chamada (comp '(a b c)) será:
(comp '(a b c))

(if (null? '(a b c)) 0 (+ 1 (comp (cdr '(a b c)))))

(+ 1 (comp '(b c)))

(+ 1 (if (null? '(b c)) 0 (+ 1 (comp (cdr '(b c))))))

(+ 1 (+ 1 (comp '(c))))

(+ 1 (+ 1 (if (null? '(c)) 0 (+ 1 (comp (cdr '(c)))))))

(+ 1 (+ 1 (+ 1 (comp '()))))

(+ 1 (+ 1 (+ 1 (if (null? '()) 0 (+ 1 (comp (cdr '())))))))

(+ 1 (+ 1 (+ 1 0)))

(+ 1 (+ 1 1))

(+ 1 2)

3 
Para definirmos uma função recursivamente,
devemos tentar identificar quatro ítens: 1) qual o caso base, 2) qual o valor da função no caso base,
3) como é a chamada recursiva, e 4) como transformar o valor
da chamada recursiva no valor final da função.
Em geral, o último item é o único que pode apresentar
alguma dificuldade.
No exemplo do fatorial, o caso base é sobre 0,
e o valor da função nesse caso é 0! = 1;
o caso recursivo é sobre n-1,
e para transformarmos (n-1)! em n! basta
multiplicarmos o primeiro valor por n.
No exemplo do comprimento da lista,
o caso base é sobre a lista vazia,
cujo comprimento é 0;
o caso recursivo é sobre o cdr da lista,
e para transformarmos o comprimento do cdr
no comprimento da lista,
temos apenas que somar 1.
Exemplo 2.1: Considere uma função que retorne uma lista de 1s com um
dado comprimento; por exemplo:
(lista-1 4)  (1 1 1 1)
(1 1 1 1)
Note que, ao contrário de comp,
que tem como domínio listas e como contra-domínio os naturais,
essa função tem como domínio os naturais e como contra-domínio listas.
Vamos tentar identificar os quatro ítens descritos acima.
Como a função recebe um número natural,
o candidato óbvio para o caso base é 0;
uma lista de 1s com comprimento 0 é exatamente a lista vazia,
isto é,
(lista-1 0)  ()
()
O caso recursivo também não é difícil,
sendo a aplicação da função sobre n-1.
Finalmente, se temos uma lista com n-1 1s,
como transformá-la em uma lista com n 1s?
Basta colocar mais um 1 na frente, com cons.
Juntando tudo temos:
(define lista-1
(lambda (n)
(if (zero? n)
'()
(cons 1 (lista-1 (- n 1))))))
Um erro bastante comum em definições recursivas
é tratarmos como caso base um caso que,
na realidade, ainda poderia ser tratado normalmente.
Por exemplo, a função lista-1 definida acima
poderia ser definida como:
(define lista-1
(lambda (n)
(if (= n 1)
'(1)
(cons 1 (lista-1 (- n 1))))))
O que há de errado com essa definição?
Em primeiro lugar, a função não funciona mais para n=0,
que é um valor perfeitamente válido para o comprimento de uma lista.
Em segundo lugar, esse caso base é algo artificial;
por que não definirmos então o caso base para n=2,
ou mesmo 3?
Várias funções têm seu comportamento naturalmente
estendido para `valores limite' como 0 ou a lista vazia,
e não há porque a implementação não tratar tais casos.
Exemplos comuns são
soma de 0 termos (que é 0, elemento neutro da soma),
produto de 0 fatores (que é 1, elemento neutro do produto),
x0 = 1 (podemos pensar em x0 como um produto de 0 fatores),
0! = 1 (idem), etc.
Por outro lado, algumas poucas funções realmente não são bem
definidas para tais valores, e neste caso devemos ajustar
nosso caso base.
Um exemplo típico é o maior elemento de uma lista;
não existe um `maior elemento' em uma lista vazia
(mais matematicamente, podemos dizer que a operação máximo
não tem elemento neutro).
Exercício 2.1: Defina as funções abaixo;
lembre-se de primeiro tentar identificar os quatro ítens
descritos acima.
- e2(n) = 2n (sendo n um número natural)
- exp(x,n) = xn
-
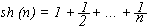
- f(n) = sin 1 + sin 2 + ... + sin n
- sf(n) = 1!+2!+ ... +n!
(dica: use a função fat definida anteriormente.)
- f(n) = sin 1 + cos 2 + sin 3 + cos 4 + ... + (sin | cos ) n
(dica: use o predicado
even? para decidir entre seno e cosseno.)
Exercício 2.2: Defina as funções abaixo;
como os parâmetros são listas,
em geral o caso base será sobre a lista vazia.
Quando o resultado da função for uma lista,
tente usar cons para construí-lo.
- uma função que retorne a soma dos elementos de uma lista de números;
- uma função que conte quantas vezes um dado elemento
aparece em uma lista;
- um predicado para verificar se um dado elemento está
presente em uma lista;6
 uma função
uma função maximo que retorne o maior elemento de
uma lista de números;
(dica: use a função pré-definida max,
que retorna o maior entre dois números dados.)
 um predicado para verificar se todos os números
de uma dada lista são pares;
um predicado para verificar se todos os números
de uma dada lista são pares;
- uma função que receba uma lista de números,
e retorne uma lista com os números incrementados de 1;
por exemplo:
(f '(1 4 6 2))  (2 5 7 3)
(2 5 7 3)
- uma função que receba uma lista de números inteiros,
e retorne uma lista contendo somente os números da lista dada que
sejam pares;
por exemplo:
(pares '(4 3 2 10 4 5))  (4 2 10 4)
(4 2 10 4)
(dica: use o predicado pré-definido
even? para testar se um número é par.)
- uma função que concatene duas listas;7
por exemplo:
(concatena '(a b c) '(d e))  (a b c d e)
(a b c d e)
Exercício 2.3: Escreva uma função que substitua todas as
ocorrências de um dado símbolo em
uma lista por outro símbolo;
por exemplo,
(substitui 'rato 'gato '(um rato maior que outro rato))  (um gato maior que outro gato)
(um gato maior que outro gato)
Exemplo 2.2:
Considere uma função ordena,
para ordenar os elementos de uma lista.
Essa função deve receber uma lista qualquer de números,
e retornar uma lista com os mesmos números em ordem crescente.
Por exemplo,
(ordena '(5 4 10 9 3 2 8))  (2 3 4 5 8 9 10)
(2 3 4 5 8 9 10)
Vamos tentar definir essa função recursivamente,
aplicando nossa regra.
O caso base natural seria a lista vazia.
Como ordenar essa lista?
Isso é fácil, é a própria lista vazia.
Vamos agora imaginar a chamada recursiva,
isto é, o valor de (ordena (cdr l)).
Juntando o que temos até agora, ficamos com algo como:
(define ordena
(lambda (l)
(if (null? l)
'()
... (ordena (cdr l)) ...)))
O que falta? Mais exatamente,
como transformar o resultado de (ordena (cdr l))
no resultado de (ordena l)?
Não é difícil perceber que precisamos inserir o primeiro elemento
da lista, (car l), na posição correta dentro
do resultado que já temos.
Vamos imaginar, temporariamente, que temos uma função para fazer isso.
Com ela, nossa função final seria:
(define ordena
(lambda (l)
(if (null? l)
'()
(insere (car l) (ordena (cdr l))))))
Temos agora que definir a função insere.
Essa função recebe um número e uma lista ordenada,
e deve inserir esse número na lista, na posição correta.
Novamente vamos usar recursão,
tentando identificar os vários casos possíveis.
Se a lista for vazia, basta colocar o número no início da lista:
(define insere
(lambda (n l)
(cond
((null? l) (cons n '()))
...)))
E se a lista não for vazia?
Nesse caso, como queremos colocar n em ordem dentro de l,
podemos comparar n com o primeiro valor de l.
Se n for menor, ele entra no início da lista e pronto.
Isso nos dá mais um caso para o cond:
((<= n (car l)) (cons n l))
Finalmente, se n for maior que o primeiro elemento de l,
basta inserirmos n em (cdr l), usando recursão,
e recolocar (car l) no início da lista:
(define insere
(lambda (n l)
(cond
((null? l) (cons n '()))
((<= n (car l)) (cons n l))
(else (cons (car l) (insere n (cdr l)))))))
Vale a pena comentarmos o exemplo acima.
Observe como resolvemos o problema da ordenação
criando um novo problema, de inserção.
Como esse novo problema era mais simples que o anterior,
tivemos um progresso, e ao resolver esse último problema,
resolvemos o primeiro.
Essa técnica é muito poderosa, pois permite resolvermos um
problema por partes, em vez de atacá-lo todo de uma vez.
Exercício 2.4: Defina uma função para inverter uma lista;8
por exemplo:
(inverte '(a b c d e))  (e d c b a)
(e d c b a)
(dica: siga os passos do exemplo anterior.
Quando necessário, defina uma função auxiliar para resolver
parte do problema.)
Definições recursivas não são usadas apenas para funções.
Na seção 1.2 definimos uma expressão como
sendo ou átomos ou uma lista de expressões entre parênteses.
Note como usamos o termo expressão,
que está sendo definido, dentro da sua definição.
Nessa definição, os átomos tem o papel de caso base.
Listas também podem ser definidas recursivamente.
Podemos definir uma lista como sendo ou 1) a lista vazia, ou 2) um elemento (o car da lista) mais uma lista
(o cdr da lista).
Exercício 2.5: Algumas funções exigem que se modifique mais
de um parâmetro na chamada recursiva.
Defina as funções abaixo:
 uma função que retorne o n-ésimo elemento de uma dada
lista, onde n é um parâmetro da função;
por exemplo:
uma função que retorne o n-ésimo elemento de uma dada
lista, onde n é um parâmetro da função;
por exemplo:
(n-esimo 3 '(a b c d e f))  c
c
Assuma que n é menor ou igual que o comprimento da lista.
- uma função que substitua o valor do n-ésimo elemento de uma
lista;
por exemplo:
(muda-n-esimo '(a b c d e f) 3 'novo)  (a b novo d e f)
(a b novo d e f)
- uma função que retorne os n primeiros elementos de uma lista
(um prefixo da lista);
por exemplo:
(primeiros 5 '(a b c d e f g h i j))  (a b c d e)
(a b c d e)
Assuma que n é menor ou igual ao comprimento da lista.
- uma função que retorne os n últimos elementos de uma lista
(um sufixo da lista).
(dica: ao invés de recursão,
procure apenas combinar as funções que você já tem.)
- dadas duas listas de números com comprimentos iguais,
retornar a lista das somas; por exemplo:
(soma-listas '(1 3 8) '(2 1 2))  (3 4 10)
(3 4 10)
-
generalize a função anterior para o caso de uma das listas ser
menor que a outra;
- um predicado que verifique se duas listas de números são iguais;
por exemplo:
(igual '(3 4 5) '(3 4 5))  #t
#t
(igual '(3 4 5) '(4 5))  #f
#f
2.1 : Recursão Final
Considere uma função para retornar o n-ésimo elemento de uma lista:
(define n-esimo
(lambda (n l)
(if (= n 1) ; primeiro elemento?
(car l)
(n-esimo (- n 1) (cdr l)))))
Considere o traço dessa função em uma situação típica:
(n-esimo 4 '(a b c d e f))
 definição + if
definição + if
(n-esimo 3 '(b c d e f))
 definição + if
definição + if
(n-esimo 2 '(c d e f))
 definição + if
definição + if
(n-esimo 1 '(d e f))
 caso base
caso base
d 
Se observarmos o traço acima,
podemos identificar uma importante diferença em relação
ao traço de uma função com recursão usual
(ver por exemplo o traço da função comp,
na página traco-comp):
a cada passo, a função é chamada com novos argumentos,
sem acumular nada extra a ser feito depois;
é como se a função estivesse sendo chamada pela primeira vez,
só que com outros argumentos.
Quando a função chega ao caso base,
não há mais nada a ser feito,
e temos direto o resultado final da função.
Isso ocorre porque, a medida que a função vai se desenrolando,
ela não cria operações pendentes,
a serem executadas após o retorno do caso base.
A chamada da função principal vai sendo simplesmente repetida,
cada vez com novos parâmetros, até chegar no caso final.
Esse tipo de recursão é chamado de
recursão final (tail recursion, em inglês).
Por causa dessas características, funções com recursão final, em geral,
são ligeiramente mais eficientes que funções com recursão normal.
Além disso, computadores têm um limite para o número de
operações pendentes que eles podem manter.
Apesar desse limite ser bastante alto
(da ordem de 103~ 104 operações),
podemos ter problemas quando manipulamos listas ou números
muito grandes usando recursão normal.
Funções que usam recursão final, como não acumulam nada,
não sofrem esse limite.
Como funções com recursão final são mais eficientes,
surge a questão de que funções podemos definir desta forma.
Algumas funções, como a ilustrada acima, são naturalmente
definidas sob a forma de recursão final.
Outras funções podem ser colocadas nessa forma,
através de algumas modificações.
Uma técnica bastante importante que podemos usar para colocar
uma função no formato de recursão final é o uso de
um acumulador.
Ela consiste em colocarmos um parâmetro extra na função que
estamos definindo,
e a cada chamada recursiva `acumular' parte do resultado
nesse parâmetro, de modo que ao chegarmos no caso base o resultado
final é exatamente o valor do acumulador,
não restando mais nada a ser feito.
Exemplo 2.3:
Uma função para somar todos os elementos de uma lista,
na sua definição usual, não usa recursão final,
pois após a chamada recursiva ainda
temos que somar o primeiro elemento da lista para obtermos
o resultado final.
Na versão mostrada abaixo, usamos um acumulador para guardar o
valor dessa soma:
(define soma
(lambda (l a)
(if (null? l)
a
(soma (cdr l) (+ a (car l))))))
Se fizermos uma chamada como (soma '(3 5 9) 0),
teremos o traço abaixo:
(soma '(3 5 9) 0)
 definição de soma + if
definição de soma + if
(soma '(5 9) 3)
 definição de soma + if
definição de soma + if
(soma '(9) 8)
 definição de soma + if
definição de soma + if
(soma '() 17)
 caso base
caso base
17  valor do acumulador
valor do acumulador
Observe como o segundo parâmetro vai acumulando o resultado,
de modo que ao chegar no caso base seu valor é o resutado final da função.
Vale a pena ressaltar que o que caracteriza a recursão final
é o fato da chamada recursiva ser a última função executada.
É essa propriedade que faz com que o traço da função tenha
a estrutura de repetição mostrada acima.
O uso de um ou mais parâmetros extras ou acumuladores
é apenas uma maneira de colocarmos uma função na forma de recursão final.
Como já observado,
muitas funções usam recursão final sem necessidade de
parâmetros extras.
Por outro lado, muitas funções podem ficar muito mais complicadas
quando escritas com recursão final.
Ao longo do texto,
vamos tratar recursão final como uma ferramenta a mais,
tentando não enfatizar nem evitar seu uso.
Exemplo 2.4:
Uma maneira de escrevermos uma função para inverter uma lista é
mostrada abaixo:
(define inverte (lambda (l a)
(if (null? l)
a
(inverte (cdr l) (cons (car l) a)))))
Que pode ser usada da seguinte forma:
(inverte '(3 4 5) '())  (5 4 3)
(5 4 3)
Note que criamos um parâmetro extra (a, no caso acima)
que começa com a lista vazia e vai acumulando o resultado
ao longo da recursão.
Quando chegamos no caso base, a resposta final está nesse acumulador.
Observando o traço dessa função,
é fácil ver o padrão característico da recursão final:
Por exemplo, para inverter a lista '(a b c) teremos:
(inverte '(a b c) '())

(inverte (cdr '(a b c)) (cons (car '(a b c) '())))

(inverte '(b c) '(a))

(inverte '(c) '(b a))

(inverte '() '(c b a))
 caso base
caso base
(c b a)  resultado final
resultado final
Novamente o segundo parâmetro acumula o resultado,
de modo que ao chegar no caso base seu valor é o resutado final da função.
Quando a recursão final necessita de parâmetros extras,
é comum definirmos uma função auxiliar para fazer a recursão final,
com os parâmetros extras,
e definir a função `principal' apenas como uma interface
que fornece os valores iniciais adequados para a função auxiliar.
Desta forma, a função principal não precisa ser chamada com
os parâmetros extras.
Seguindo essa idéia, a função inverte seria definida
como:
(define inverte-aux (lambda (l a)
(if (null? l)
a
(inverte-aux (cdr l) (cons (car l) a)))))
(define inverte (lambda (l) (inverte-aux l '())))
Temos aqui mais um exemplo de abstração:
com esse método, quem usa a função pode abstrair
(e portanto, não se preocupar com) a possível
existência de parâmetros extras na função.
Exercício 2.6: (Re)escreva as funções abaixo usando recursão final:
- fat(n) = n!
- exp(x,n) = xn (sendo n um número natural)
-
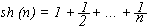
- f(n) = sin 1 + sin 2 + ... + sin n
- sf(n) = 1!+2!+ ... +n!
(dica: use a função fat definida anteriormente.)
- uma função
comp que retorne o comprimento de uma lista
- uma função
conta que retorne o número de vezes que um dado
símbolo aparece em uma lista.
- uma função
maximo que retorne o maior
elemento de uma lista de números.
 uma função
uma função pos que retorne em que
posição um elemento ocorre em uma lista
(ou '() se ele não estiver presente na lista).
Por exemplo,
(pos 'melao '(abacaxi melao banana pera))  2
2
(pos 'uva '(abacaxi melao banana pera))  ()
()
- uma função que retorne uma lista crescente de números
com um dado comprimento; por exemplo:
(ld 5)  (1 2 3 4 5)
(1 2 3 4 5)
Exercício 2.7:  Escreva uma função para calcular
Escreva uma função para calcular
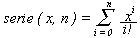 usando recursão final.
(dica: use três acumuladores: um para o somatório,
outro para o fatorial, e o terceiro para a exponenciação.)
Exercício 2.8:
A série de Fibonacci é definida como
0, 1, 1, 2, 3, 5, 8, 13, 21, ...
onde cada termo é a soma dos dois termos anteriores,
isto é,
usando recursão final.
(dica: use três acumuladores: um para o somatório,
outro para o fatorial, e o terceiro para a exponenciação.)
Exercício 2.8:
A série de Fibonacci é definida como
0, 1, 1, 2, 3, 5, 8, 13, 21, ...
onde cada termo é a soma dos dois termos anteriores,
isto é,
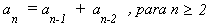
- Escreva uma função recursiva
fib
que calcule o n-ésimo termo da série de Fibonacci.
Não use recursão final; baseie sua função na equação acima.
- Você tem alguma esperança de calcular
(fib 40) com sua
função? Por que?
(Veja quanto tempo sua função demora para calcular (fib n),
para n pouco maior que 20).
- Reescreva a função
fib usando recursão final,
e compare a eficiência das duas implementações.
(dica: use dois parâmetros adicionais,
para passar adiante os dois últimos termos da série.)
2.2 : Indução
Quando discutimos funções,
vimos que, quando raciocinamos sobre uma função,
podemos pensar na sua execução de duas formas:
concreta e abstrata.
A forma concreta corresponde a seguirmos o traço de execução
dentro da função, executando cada passo dela,
como o computador sempre faz.
A forma abstrata pode ser usada quando assumimos que a função
está correta e sabemos o que ela calcula;
nesse caso, podemos passar direto da chamada para o resultado.
É a forma abstrata que permite executarmos mentalmente um passo
como
(+ 8 (sin 5))  (+ 8 -0.958924)
(+ 8 -0.958924)
sem nem mesmo sabermos como a função sin é implementada.
A mesma visão abstrata que usamos em chamadas comuns
pode ser aplicada sobre funções recursivas.
A idéia por trás disso é que uma chamada recursiva é,
em muitos aspectos, similar a uma chamada não recursiva.
Como exemplo, vamos voltar a função fatorial.
Suponha que queremos saber o valor de (fat 6);
o traço dessa chamada poderia ser escrito como:
(fat 6)
 definição concreta de
definição concreta de fat
(* 6 (fat 5))
 definição abstrata de
definição abstrata de fat (5!=120)
(* 6 120)
 aritmética
aritmética
720  resultado final (igual a 6!)
resultado final (igual a 6!)
Essa visão abstrata é fundamental quando queremos verificar
se uma função está escrita corretamente.
Imagine que queremos nos certificar que nossa implementação da
função fatorial está correta, isto é,
para qualquer n 0 temos que
0 temos que
(fat n)  n!
n!
Fazendo o traço para diversos valores de n,
ou executando a função no computador,
podemos ganhar mais confiança em nossa definição,
mas não podemos provar que ela está correta,
pois não podemos fazer o traço concreto da função para
todos os possíveis valores de n.
Para verificarmos e/ou nos certificarmos que uma função está
escrita corretamente,
o primeiro passo é colocar claramente qual
a pré-condição da função.
No nosso exemplo, não esperamos que chamadas como
(fat -5) ou (fat '(a b c)) funcionem.
Ou seja, a pré-condição para uma chamada (fat n) é
que n seja um número natural (um inteiro maior ou igual a 0).
Em seguida, fazemos o traço da função para um valor
abstrato de n.
Como n estará representando qualquer valor que
satisfaça a pré-condição,
toda vez que tivermos uma seleção na nossa função
(ifs ou conds)
iremos fazer um traço separado para cada caso.
Voltando ao nosso exemplo,
como a função fat tem dois casos,
iremos fazer dois traços:
no primeiro caso, temos n=0, e o traço fica trivial:
(fat 0)
 definição concreta de
definição concreta de fat
(if (zero? 0) 1 (* 0 (fat (- 0 1))))
 seleção
seleção
1  resultado final
resultado final
Esse caso está correto, pois sabemos que 0!=1;
logo temos que
(fat 0)  0!
0!
No segundo caso, imaginamos um n qualquer maior que 0,
e fazemos o seu traço.
Note o uso de itálico para indicar os valores abstratos
dentro das expressões:
(fat n)
 definição concreta de
definição concreta de fat (com n 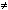 0)
0)
(* n (fat (n-1)))
 definição abstrata de
definição abstrata de fat:
(fat (n-1))  (n-1)!
(n-1)!
(* n (n-1)!)
 aritmética
aritmética
n × (n-1)!  resultado final
resultado final
Ou seja, temos que
(fat n)  n × (n-1)! =
n × ((n-1) × ... × 1) = n!
n × (n-1)! =
n × ((n-1) × ... × 1) = n!
Como isso vale para qualquer n>0,
e já vimos também o caso n=0,
podemos afirmar que
(fat n)  n!
n!
para qualquer n 0.
Esse raciocínio está correto, ou estamos blefando?
Afinal, estamos usando o fato que
0.
Esse raciocínio está correto, ou estamos blefando?
Afinal, estamos usando o fato que
(fat (n-1)) (n-1)!
para chegarmos a
(n-1)!
para chegarmos a (fat n) n!.
Não estamos andando em círculos?
A justificativa para o raciocínio que utilizamos é chamada
de princípio de indução.
Segundo o princípio de indução,
quando estamos verificando se uma função está corretamente definida,
podemos assumir que qualquer chamada recursiva da função
retornará a resposta correta,
desde que a função seja chamada com valores adequados
à sua pré-condição e
que a função termine.9
Antes de continuarmos,
é importante frizar que esse problema não é apenas teórico:
a função fatorial é muito simples, quase trivial,
mas para funções mais complexas pode ser bastante complicado
nos certificarmos que escrevemos a função corretamente.
Além disso, um programador experiente não pensa `concretamente'
sobre programas, mas abstratamente, ou indutivamente.
Ilustrativamente, podemos dizer que o programador iniciante,
é o que vê 120! como
120 × 119 × 118 × 117 × ...
× 5 × 4 × 3 × 2 × 1,
enquanto um programador experiente vê 120! como 120 × 119!.
n!.
Não estamos andando em círculos?
A justificativa para o raciocínio que utilizamos é chamada
de princípio de indução.
Segundo o princípio de indução,
quando estamos verificando se uma função está corretamente definida,
podemos assumir que qualquer chamada recursiva da função
retornará a resposta correta,
desde que a função seja chamada com valores adequados
à sua pré-condição e
que a função termine.9
Antes de continuarmos,
é importante frizar que esse problema não é apenas teórico:
a função fatorial é muito simples, quase trivial,
mas para funções mais complexas pode ser bastante complicado
nos certificarmos que escrevemos a função corretamente.
Além disso, um programador experiente não pensa `concretamente'
sobre programas, mas abstratamente, ou indutivamente.
Ilustrativamente, podemos dizer que o programador iniciante,
é o que vê 120! como
120 × 119 × 118 × 117 × ...
× 5 × 4 × 3 × 2 × 1,
enquanto um programador experiente vê 120! como 120 × 119!.
Exemplo 2.5: Considere a função abaixo,
para calcular xn usando um acumulador e recursão final:
(define exp
(lambda (x n a)
(if (zero? n)
a
(exp x (- n 1) (* x a)))))
A terminação de exp é trivialmente garantida,
pois a cada chamada decrementamos n,
e paramos quando n=0.
A pré-condição dessa função é que x e a
sejam números reais quaisquer,
e n um inteiro maior ou igual a zero.
Mas para verificarmos que exp realmente calcula xn,
precisamos colocar o papel de a mais claro.
Em particular, o que ocorre se chamarmos (exp x n a)
com um a qualquer?
Não é difícil perceber que a função deveria retornar a × xn;
portanto, o que devemos verificar é que
(exp x n a)  a × xn
a × xn
No caso base, com n=0, temos que
(exp x 0 a)  a = a × x0
a = a × x0
que está correto.
No caso geral, com n>0, temos que
(exp x n a)  (exp x (n-1) (x × a))
(exp x (n-1) (x × a))
Aqui usamos a hipótese de indução no passo,
e um pouco de aritmética na igualdade,
para chegarmos em:
(exp x (n-1) (x × a))  (x × a) × xn-1=a × xn
(x × a) × xn-1=a × xn
Finalmente, se juntarmos tudo e fixarmos a=1,
teremos:
(exp x n 1)  1 × xn = xn
1 × xn = xn
Exemplo 2.6: Considere a função abaixo (incorreta), para calcular 2n:
(define f
(lambda (n)
(if (zero? n)
1
(/ (f (+ n 1))))))
Para n=0, temos
(f 0)  1=20
1=20
como queríamos.
Para n>0, temos
(f n)  (/ (f (n+1)) 2)
(/ (f (n+1)) 2)
Usando o princípio de indução aqui,
conseguiríamos provar trivialmente que
(f n)  2n+1/2 = 2n
2n+1/2 = 2n
Mas não é muito difícil perceber que essa função não funciona,
donde há algo errado em nosso raciocínio.
Se chamarmos essa função com o argumento 5, por exemplo,
teremos o traço abaixo:
(f 5)

(/ (f 6) 2)

(/ (/ (f 7) 2) 2)

(/ (/ (/ (f 8) 2) 2) 2)

... 
A função ficará se repetindo infinitamente,
em uma situação que chamamos de loop.
Como a função não termina,
não podemos usar o princípio de indução.
2.3 : Terminação
Muitas vezes, é bastante fácil verificarmos que
uma função não vai entrar em loop.
Funções como fatorial, com valor 0 de caso base e
que decrementam em 1 seu argumento a cada chamada recursiva,
sempre terminam quando chamadas com um argumento positivo,
pois qualquer número natural chega a 0 após um
certo número de decrementos.
Entretanto, nem todas funções recursivas são como a função fatorial.
Para funções mais complexas,
o problema de garantirmos que a função não entra em loop
pode ser difícil, ou mesmo impossível, de resolver.
Como regra geral, para nos certificarmos que uma função f termina,
precisamos conseguir uma função h sobre os parâmetros
da função f tal que 1) h é sempre um número inteiro maior ou igual que 0, e 2) h decresce a cada nova chamada recursiva.
Podemos pensar em h como uma medida do tamanho do problema.
O argumento é que, se f entrasse em loop,
teríamos uma sequência infinita de valores de h,
onde todos os valores são inteiros positivos e cada novo valor é
estritamente menor que o anterior.
Como tal sequência é impossível, a função tem que terminar.10
No caso da função fatorial, podemos fazer a opção
trivial de h(n)=n.
Como a pré-condição de fat é n 0,
a condição 1 é satisfeita;
além disso, como a chamada recursiva é sobre n-1,
a condição 2 também é satisfeita.
Para muitas funções sobre listas,
podemos definir h como o comprimento da lista.
O comprimento é sempre um inteiro positivo (condição 1),
e
0,
a condição 1 é satisfeita;
além disso, como a chamada recursiva é sobre n-1,
a condição 2 também é satisfeita.
Para muitas funções sobre listas,
podemos definir h como o comprimento da lista.
O comprimento é sempre um inteiro positivo (condição 1),
e (cdr l) tem sempre um comprimento
menor que o comprimento de l (condição 2).
Exemplo 2.7: O algoritmo de Euclides, para calcular o MDC
(Máximo Divisor Comum) entre dois números,
se baseia nas igualdades mdc(a,0) = a, mdc(0,b) = b,
mdc(a,b)=mdc(a-b,b), se a b,
e mdc(a,b)=mdc(a,b-a), se b
b,
e mdc(a,b)=mdc(a,b-a), se b a.
Sua implementação em Scheme pode ser escrita como:
a.
Sua implementação em Scheme pode ser escrita como:
(define mdc
(lambda (a b)
(cond
((zero? a) b)
((zero? b) a)
((>= a b) (mdc (- a b) b))
(else (mdc a (- b a))))))
A pré-condição para mdc é que a e b sejam números
naturais (isto é, inteiros maiores ou iguais a 0).
Para provarmos que essa função está correta,
temos que verificar 4 casos.
Note que (mdc a b) denota nossa função,
definida em Scheme,
enquanto mdc(a,b) denota a função matemática de Máximo Divisor Comum.
- a=0 --- Nesse caso,
(mdc 0 b)  b=mdc(0,b).
b=mdc(0,b).
- b=0 --- Idêntico ao caso anterior.
- a
 b --- Nesse caso,
b --- Nesse caso,
(mdc a b)  (mdc (a-b) b)
(mdc (a-b) b)
Como a  b, temos que a-b
b, temos que a-b  0,
garantindo a pré-condição na chamada recursiva.
Pelo princípio de indução,
0,
garantindo a pré-condição na chamada recursiva.
Pelo princípio de indução,
(mdc (a-b) b)  mdc(a-b,b)
mdc(a-b,b)
Mas sabemos (vide acima) que mdc(a-b,b)=mdc(a,b),
logo temos que
(mdc a b)  mdc(a,b)
mdc(a,b)
- a<b --- Idêntico ao caso anterior.
Portanto, usando o princípio da indução não é difícil
nos certificarmos que nossa função está correta,
desde que ela termine.
Para nos convencermos da terminação da função mdc,
podemos definir h como h(a,b)=a+b.
Como a e b são sempre positivos (pré-condição da função), temos que 1) h(a,b)=a+b  0.
Como a chamada recursiva só é feita se a e b forem
maiores que 0,
temos que a subtração necessariamente diminui seus valores. Portanto, 2) a cada nova chamada a soma a+b será menor que na
chamada anterior.
Logo, como vimos acima, a função termina.
0.
Como a chamada recursiva só é feita se a e b forem
maiores que 0,
temos que a subtração necessariamente diminui seus valores. Portanto, 2) a cada nova chamada a soma a+b será menor que na
chamada anterior.
Logo, como vimos acima, a função termina.
Exercício 2.9: Faça o traço da chamada (mdc 12 30).
Exercício 2.10: Uma definição mais tradicional para o algoritmo de Euclides se
baseia nas igualdades mdc(a,0) = a, mdc(a,b)=mdc(b,a),
e mdc(a,b)=mdc(a-b,b), se a b.
b.
- Defina a função
mdc em Scheme usando essas igualdades.
- Mostre que sua função sempre termina quando chamada com
argumentos positivos.
Exemplo 2.8: Existem alguns casos em que a terminação pode
ser uma questão sem resposta conhecida.
A função abaixo, por exemplo, é famosa por esse motivo:
(define collatz
(lambda (n)
(cond
((= n 1) '())
((even? n) (cons n (collatz (quotient n 2))))
(else (cons n (collatz (+ (* n 3) 1)))))))
Exercício 2.11: Implemente a função collatz,
e calcule seu valor para os argumentos 15, 23, 27 e 28.
Você consegue estabelecer alguma relação entre o argumento e o
comprimento da resposta?
Existe algum n natural para o qual essa função fica em loop?
Exercício 2.12: Considere a função abaixo,
para calcular o produto de dois números naturais:
(define mult
(lambda (a b)
(cond
((zero? b) 0)
((even? b) (* 2 (mult a (quotient b 2))))
(else (+ a (* 2 (mult a (quotient b 2))))))))
Mostre que essa função sempre termina quando chamada com a,b 0,
e que
0,
e que
(mult a b)  a × b
a × b
Exercício 2.13:  Escreva uma função que retorne a lista dos fatores
primos de um dado número.
Por exemplo,
Escreva uma função que retorne a lista dos fatores
primos de um dado número.
Por exemplo,
(fatores 84)  (2 2 3 7)
(2 2 3 7)
Use a expressão (zero? (remainder x y)) para testar
se x é divisível por y.
Mostre que sua função sempre termina quando chamada
com n 0, e que o produto dos elementos
da lista retornada é igual a n.
0, e que o produto dos elementos
da lista retornada é igual a n.
2.4 : Padrões de Recursão
Muitas das funções recursivas definidas ao longo deste capítulo
seguem determinados padrões.
Isto é, muitas das funções que vimos são bastante parecidas entre si,
compartilhando uma estrutura comum,
e diferindo apenas em alguns poucos pontos.
Nesta seção, vamos tentar identificar alguns dos padrões mais comuns,
e mostrar como podemos definir funções em Scheme que refletem
cada padrão.
A identificação de padrões em programas é altamente benéfica.
Em primeiro lugar, é uma fonte de soluções de problemas.
Geralmente, quando temos que escrever uma função ou programa
para uma determinada tarefa, a primeira pergunta que nos fazemos é:
`será que eu já não fiz ou ví algo parecido antes?'.
A nossa bagagem de padrões conhecidos,
que adquirimos ao longo do tempo,
nos permite resolver um grande número de problemas de
forma quase imediata.
Em segundo lugar, muitos padrões podem ser diretamente
programados na linguagem.
Com isso, ao identificarmos que um determinado problema pode
ser resolvido com um determinado padrão,
não precisamos nem mesmo escrever toda a solução,
mas apenas usar a função já existente.
O primeiro padrão que vamos estudar é chamado filtro.
Considere a função abaixo,
para filtrar os elementos pares de uma lista:
(define filtra-pares
(lambda (l)
(cond
((null? l) '())
((even? (car l)) (cons (car l) (filtra-pares (cdr l))))
(else (filtra-pares (cdr l))))))
Dada uma lista de números, filtra-pares retorna
uma nova lista com apenas os números pares da lista original.
Exercício 2.14: Escreva uma função filtra-impar,
que retorne uma lista com apenas os números ímpares da lista original
(isto é, filtre os elementos ímpares).
Exercício 2.15: Escreva uma função filtra-10,
que filtre os elementos maiores que 10.
Exercício 2.16: As funções filtra-par, filtra-impar e filtra-10
são semelhantes? Por que?
Em que elas diferem?
Podemos literalmente abstrair as
diferenças entre essas funções.
Em vez de uma função com um teste concreto,
fixo, como por exemplo even?,
criamos uma função genérica filtra,
onde o predicado de teste é mais um parâmetro da função:
(define filtra
(lambda (f l) ; f e' o predicado de filtro
(cond
((null? l) '())
((f (car l)) (cons (car l) (filtra f (cdr l))))
(else (filtra f (cdr l))))))
Assim, para filtrarmos os números pares de uma lista,
podemos executar
(filtra even? '(1 10 9 45 22 11 0))  (10 22 0)
(10 22 0)
Exercício 2.17: Use a função filtra para filtrar os seguintes
elementos de uma lista:
- elementos ímpares;
- elementos maiores que 10;
(dica: você não precisa definir um novo predicado.
Ao invés disso, você pode usar
lambda diretamente na chamada:
pense na função (lambda (x) (> x 10)).)
- elementos no intervalo [5,15].
Exemplo 2.9:
O predicado filtra permite uma definição bastante interessante
para a função ordena, que ordena os elementos de uma dada lista
em ordem crescente.
Dada uma lista não vazia l,
o algoritmo usa filtra para dividir (cdr l) em
duas partes, uma com os elementos menores
que (car l) e a outra com os elementos maiores que (car l).
Essas duas listas são então ordenadas de forma independente
com chamadas recursivas de ordena.
Finalmente, as duas sub-listas ordenadas e (car l)
são reunidos em uma única lista com a função append e cons.
(define (ordena l)
(if (null? l)
'()
(append
(ordena (filtra (lambda (x) (<= x (car l))) (cdr l)))
(cons (car l)
(ordena (filtra (lambda (x) (> x (car l))) (cdr l)))))))
Um outro padrão bastante comum é o mapeamento,
que são funções que recebem uma lista e retornam outra lista,
formada pelos elementos da lista original transformados de alguma forma.
Esse padrão pode ser capturado pela função genérica mapeia.
Essa função recebe uma função f e uma lista,
e retorna a lista dos resultados da aplicação de f
sobre cada elemento da lista.11
Por exemplo, para arredondarmos todos os números de uma lista,
podemos chamar
(mapeia round '(1.3 5.01 3.32))  (1 5 3)
(1 5 3)
onde round é uma função pré-definida que arredonda um
número real.
Exercício 2.18: Escreva a função mapeia.
Exercício 2.19: Usando mapeia, escreva as funções abaixo.
Não use recursão.
- uma função
ls que receba uma lista de números
e retorne a lista de seus senos.
- uma função
q que receba uma lista
de números e retorne a lista de seus quadrados.
Por exemplo,
(q '(3 9 2))  (9 81 4)
(9 81 4)
Exercício 2.20:
Escreva uma função que calcule o somatório dos elementos de uma lista;
use recursão final.
Em seguida, escreva uma função que calcule o produto dos
elementos de uma lista, também usando recursão final.
Qual a semelhança entre essas duas funções? Quais as diferenças?
Generalize as duas em uma função acumula,
que receba como parâmetro, além da lista e do acumulador,
a operação a acumular (+, *, etc).
Exercício 2.21: Usando a função acumula,
defina funções para as tarefas abaixo.
Não use recursão.
- calcular o maior elemento de uma lista;
- calcular o menor elemento de uma lista;

 calcular o comprimento de uma lista;
calcular o comprimento de uma lista;
 contar quantas vezes um dado número aparece em uma lista;
contar quantas vezes um dado número aparece em uma lista;
- inverter uma lista.
Exercício 2.22:  Usando a função
Usando a função acumula, escreva um predicado genérico,
que receba um predicado e uma lista,
e verifique se todos os elementos da lista satisfazem o
predicado dado.
Por exemplo,
(acpred even? '(2 3 4 6))  #f
#f
(acpred odd? '(3 19 7 1))  #t
#t
Exercício 2.23:  Identifique alguma função recursiva já
implementada por você que não possa ser reescrita sem o uso de recursão,
usando-se
Identifique alguma função recursiva já
implementada por você que não possa ser reescrita sem o uso de recursão,
usando-se filtra, mapeia, e acumula.
2.5 : Repetições
Scheme oferece uma outra forma de definirmos funções com recursão final,
onde é realçado o aspecto repetitivo da recursão final
e um padrão estrutural bastante comum nesse tipo de recursão.
Vamos começar revendo uma típica função com recursão final.
Considere as definições abaixo,
para somar os elementos de uma lista:
(define soma-aux
(lambda (l s)
(if (null? l)
s
(soma-aux (cdr l) (+ s (car l))))))
(define soma (lambda (ll) (soma-aux ll 0)))
Se analisarmos a estrutura da função soma,
podemos identificar vários elementos,
comuns à maioria das funções com recursão final:
- Os parâmetros da função original,
no exemplo apenas
ll,
que são passados inalterados para soma-aux.
- Os parâmetros de
soma-aux, ou variáveis, l e s.
- Os valores iniciais que damos aos parâmetros de
soma-aux,
no caso ll e 0.
- As expressões de atualização,
que definem os novos valores dos parâmetros
a cada nova chamada recursiva.
No exemplo acima, essas expressões são
(cdr l) (para l)
e (+ s (car l)) (para s).
- O teste de terminação,
(null? l).
- O valor final da função, que é o valor final de
s.
Exercício 2.24: Identifique cada um dos elementos acima na função definida
no exemplo 2.4
Se fizermos o traço da chamada (soma '(4 8 1 -3)),
teremos:
(soma '(4 8 1 -3))

(soma-aux '(4 8 1 -3) 0)

(soma-aux '(8 1 -3) 4)

(soma-aux '(1 -3) 12)

(soma-aux '(-3) 13)

(soma-aux '() 10)

l é nula, retorna valor de s
10  valor de s
valor de s
Observe como, nesse traço, temos uma repetição de passos,
onde apenas os valores de l e de s vão mudando a
cada passo.
Funções com recursão final podem ser escritas de uma forma
em que esse caráter repetitivo fique mais explícito,
através da construção do.
Seguindo nosso exemplo,
podemos reescrever a função soma
usando a construção do,
como mostrado abaixo:
(define soma
(lambda (ll)
(do ([l ll (cdr l)]
[s 0 (+ s (car l))])
((null? l) s))))
observação: novamente
usamos colchetes [...]
no lugar de parênteses (...),
de modo a deixar mais claro o formato do do.
Novamente, em qualquer uso real esses colchetes devem
ser substituídos por parênteses.
Note como os mesmos elementos identificados na
implementação recursiva estão presentes aqui,
agrupados de uma forma diferente.
O primeiro argumento do do é uma lista,
onde colocamos o que seriam os parâmetros variáveis
na definição recursiva;
junto colocamos seu valor inicial e a expressão de atualização,
usada para se calcular o próximo valor.
Assim, o primeiro item dessa lista,
(l ll (cdr l))
define uma variável l,
que começa a repetição com o valor de ll,
e a cada passo recebe um novo valor (cdr l).
Da mesma forma, o segundo item,
(s 0 (+ s (car l)))
cria uma variável s, com valor inicial igual a 0,
e que a cada novo passo recebe o valor da expressão
(+ s (car l)).
O segundo argumento do do é outra lista,
cujo primeiro item é o teste de terminação,
e o segundo é o valor final do do.
No exemplo acima,
esse argumento é a lista ((null? l) s).
A sintaxe geral da construção do é mostrada abaixo:
(do ([n1 v1 e1]
...
[nn vn en])
(teste valor-final))
Nessa construção, cada grupo [ni vi ei]
cria uma nova variável chamada ni,
que começa a repetição com valor vi,
e a cada passo recebe um novo valor dado por ei.
O teste é um predicado qualquer;
enquanto ele for falso,
o do continuará executando passos.
Finalmente, quando teste for verdadeiro,
a execução do do termina,
resultando no valor da expressão valor-final.
Mais formalmente, a sintaxe geral de do mostrada
acima é equivalente a:
(define aux
(lambda (n1 ... nn)
(if teste
valor-final
(aux e1 ... en))))
(aux v1 ... vn) ; <= expressao equivalente ao do
Exemplo 2.10:
Vamos definir, usando do,
uma função para calcular a média dos elementos
de uma lista de números:
(define (media l)
(do ((l1 l (cdr l1))
(s 0 (+ s (car l1)))
(n 0 (+ n 1)))
((null? l1) (/ s n))))
Nessa função,
temos uma variável l1, que começa com o valor de l,
e a cada repetição se torna (cdr l1);
temos também uma variável s que é inicada com 0
e que a cada passo recebe (+ s (car l1));
e temos uma terceira variável n,
iniciada também com 0 e evoluindo com (+ n 1).
O teste de parada é dado pela expressão (null? l1),
e o valor final do do (e da função) será o valor
da expressão (/ s n).
Exercício 2.25:  Reescreva a função
Reescreva a função media apresentada
no exemplo anterior usando recursão final.
Preserve todos os elementos usados na versão com do.
O traço de um do pode ser feito meramente acompanhando-se
a evolução de suas variáveis.
Assim, o traço de uma função definida com do e sua
equivalente definida com recursão final são bastante parecidos.
Mas é importante frizarmos que a construção do,
apesar de ter o mesmo comportamento de funções com recursão final,
não implica em chamadas de função na sua execução.
Exemplo 2.11: Considere a definição de media dada no exemplo 2.10.
Vamos fazer o traço da chamada (media '(3 4 2)):
(media '(3 4 2))

do, valores iniciais
(do '(3 4 2) 0 0)

l1 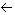 (cdr l1)
(cdr l1),
s  (+ s (car l1))
(+ s (car l1)),
n  (+ n 1)
(+ n 1)
(do '(4 2) 3 1)

l1  (cdr l1)
(cdr l1),
s  (+ s (car l1))
(+ s (car l1)),
n  (+ n 1)
(+ n 1)
(do '(2) 7 2)

l1  (cdr l1)
(cdr l1),
s  (+ s (car l1))
(+ s (car l1)),
n  (+ n 1)
(+ n 1)
(do '() 9 3)
 predicado
predicado (null? l1) verdadeiro,
termina com valor (/ s n)
3 
Exercício 2.26: Faça novamente o traço da chamada (media '(3 4 2)),
mas usando a definição recursiva de media,
feita no exercício 2.25.
Compare os dois traços.
Exercício 2.27: (Re)escreva as rotinas abaixo usando do;
se quiser, escreva antes a função com recursão final,
e depois transforme.
- fat(n) = n!
- exp(x,n) = xn (sendo n um número natural)
-
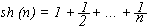
- f(n) = sin 1 + sin 2 + ... + sin n
- uma função
comp que retorne o comprimento de uma lista
- uma função
som que retorne o somatório de uma lista de números.
- uma função
inverte que retorne uma dada lista invertida.
 uma função
uma função conta que retorne o
número de vezes que um dado símbolo aparece em uma lista;
Exercício 2.28: Reescreva a função acumula, do exercício 2.20,
usando do.
Capítulo 3 :
Representação de Dados
Até agora, todas as funções que definimos trabalhavam sobre
números e listas.
Entretanto, um computador não manipula apenas esses tipos de dados;
um computador é capaz de tratar conjuntos, imagens, matrizes, sons,
enfim, uma variedade ilimitada de tipos de informação.
Como um computador pode manipular todos esses tipos de informação,
e como uma linguagem pode nos oferecer todos esses tipos?
Temos aqui uma questão similar a que já encontramos com funções.
Lá, a questão era: como uma linguagem pode oferecer todas as
funções que precisamos?
E a solução era que, ao invés de fornecer todas as funções que precisamos,
uma linguagem deve oferecer mecanismos para criarmos novas funções.
Da mesma forma,
uma linguagem não pode nos oferecer todos os tipos
de dados que precisamos.
Ao contrário, mais importante que os tipos básicos que ela oferece
são os mecanismos oferecidos para criarmos novos tipos.
Uma das tarefas mais importantes de programação é decidirmos
como cada informação que precisamos tratar
deverá ser representada no computador,
através da linguagem que utilizamos.
Em Scheme, o principal mecanismo para a construção
de novos tipos é a lista.
Neste capítulo, vamos ver como listas podem ser
usadas para representar diversos tipos de informação diferentes,
como conjuntos, catálogos, polinômios, expressões aritméticas,
e mesmo números naturais.
Outro mecanismo importante para representação de dados,
o vetor, será visto no capítulo proc.
3.1 : Representando Conjuntos
Uma grande variedade de dados podem ser representados através
do conceito matemático de conjuntos.
Por exemplo,
um programa de controle acadêmico
pode utilizar conjuntos para armazenar
as disciplinas cursadas por um aluno,
os pré-requisitos de uma disciplina,
os alunos de cada curso, etc.
Uma maneira bastante direta para se representar conjuntos
em Scheme é através de uma lista de seus elementos.
Note que um mesmo conjunto pode ser representado por várias listas;
por exemplo, o conjunto {a,b} pode ser representado pelas listas
(a b),
(b a),
(a b a),
etc.
De modo a diminuir um pouco essa multiplicidade,
vamos exigir que uma lista representando um conjunto nunca
tenha elementos repetidos
(esse tipo de restrição sobre possíveis representações de
um valor é denominado invariante).
Assim, as listas (a b) e (b a) ambas representam o conjunto
{a,b},
enquanto (a b a) não é uma representação válida de nenhum conjunto
(pois não satisfaz o invariante).
Mais do que armazenar dados,
um computador deve ser capaz de manipular esses dados.
Assim, mais importante do que definirmos como representar um
determinado tipo de dado,
é mostrarmos como podemos manipular dados usando essa representação.
Vamos então mostrar como as diversas operações básicas de conjuntos
podem ser definidas sobre a representação com listas.
A operação mais básica sobre conjuntos é o predicado pertence?,
para verificar se um dado elemento pertence a um conjunto.
Sua definição não apresenta dificuldades:
(define pertence?
(lambda (e c)
(if (null? c)
#f
(or (equal? e (car c))
(pertence? e (cdr c))))))
No caso base, com o conjunto vazio, a função resulta em falso
(nenhum elemento pode pertencer ao conjunto vazio).
Se a lista não é vazia, um elemento na lista ou é igual ao primeiro
elemento ou então está no resto da lista.
A união de dois conjuntos já não é tão direta.
Podemos pensar em simplesmente concatenar as duas listas,
mas se existirem elementos comuns aos dois conjuntos,
eles apareceriam repetidos na lista final,
desrespeitando nosso invariante.
Para evitarmos esse problema, temos que tomar o cuidado
de somente inserir um novo elemento no resultado se ele
ainda não estiver lá:
(define uniao
(lambda (a b)
(cond
((null? a) b)
((pertence? (car a) b) (uniao (cdr a) b))
(else (cons (car a) (uniao (cdr a) b))))))
Exercício 3.1: Faça o traço da chamada (uniao '(a b c) '(b e)).
Exercício 3.2: Escreva uma função que receba dois conjuntos e retorne sua interseção.
Exercício 3.3: Escreva uma função que receba dois conjuntos e
retorne sua diferença.
(A diferença entre dois conjuntos A e B, A-B,
é o conjunto formado pelos elementos de A que não pertencem a B.)
Exercício 3.4: Escreva um predicado que receba dois conjuntos c1 e c2 e verifique
se c1  c2.
Exercício 3.5: Escreva um predicado que receba dois conjuntos c1 e c2 e verifique
se c1 = c2.
Observe que não basta comparar as listas.
Por exemplo, os conjuntos representados pelas listas
c2.
Exercício 3.5: Escreva um predicado que receba dois conjuntos c1 e c2 e verifique
se c1 = c2.
Observe que não basta comparar as listas.
Por exemplo, os conjuntos representados pelas listas
(1 2 3) e (2 3 1) são iguais.
(dica: lembre-se que c1 = c2 se e somente se
c1  c2 e c2
c2 e c2  c1.)
Exercício 3.6: Redefina as funções de união e interseção de conjuntos
usando
c1.)
Exercício 3.6: Redefina as funções de união e interseção de conjuntos
usando do.
Exercício 3.7:  Reescreva as funções de união e interseção de conjuntos utilizando
a função
Reescreva as funções de união e interseção de conjuntos utilizando
a função acumula, do exercício 2.20.
3.2 : Representação de Números Naturais
Vamos imaginar que nossa linguagem ou nosso computador
não tivesse uma maneira interna de representar números.
Uma maneira bastante simples de representar os números naturais
seria através de listas de átomos,
onde o comprimento da lista corresponderia ao natural representado.
Assim,
o número 1 seria representado por (1),
o número 2 por (1 1),
e assim sucessivamente.
Essa maneira de se representar números naturais é comumente
chamada de notação unária.
Com essa representação,
poderíamos definir algumas operações primitivas sobre
naturais de maneira bastante direta.
O número 0 seria representado pela lista vazia,
(define zero '())
Um predicado para verificar se um número é zero seria:12
(define zer? (lambda (n) (null? n)))
ou mais diretamente:
(define zer? null?)
A operação de incrementar 1 seria:
(define inc (lambda (n) (cons 1 n)))
e a operação de decrementar 1:
(define dec (lambda (n) (cdr n)))
A princípio, as definições acima podem parecer algo inúteis,
dado que as funções são tão simples,
no caso de zer? sendo apenas outro nome para null?.
Entretanto, isso é uma aplicação direta de nossa
forma básica de abstração, que é dar nomes às coisas.
O benefício principal ao definirmos essas funções é
o que chamamos de abstração de dados,
pois abstraimos como os dados estão sendo representados.
Com o conjunto básico de operações
zero, zer?, inc e dec,
podemos definir todas as operações aritméticas usuais,
sem nos preocuparmos com que representação estamos usando.
A operação para somar dois números pode ser definida como:
(define soma
(lambda (a b)
(if (zer? b)
a
(inc (soma a (dec b))))))
ou alternativamente, com recursão final:
(define soma
(lambda (a b)
(do ((a1 a (inc a1))
(b1 b (dec b1)))
((zer? b1) a1))))
Observe como toda a manipulação dos números é feita através
das funções básicas;
não existe nenhuma referência ao fato dos números estarem
sendo representados por listas.
Podemos escrever e entender a função soma sem saber
como os números estão sendo representados.
De fato, podemos redefinir nossa representação de números,
para usarmos a representação normal de Scheme, como mostrado abaixo:
(define zero 0)
(define zer? zero?)
(define inc (lambda (n) (+ n 1)))
(define dec (lambda (n) (- n 1)))
e a função soma definida acima continuará
funcionando corretamente.
Exercício 3.8: Defina as funções abaixo, para operarem sobre dois
naturais dados na representação unária.
Como na definição de soma,
não faça referência à representação por listas;
use apenas as operações sobre números definidas anteriormente.
- Uma função
sub,
para subtrair dois números.
Por exemplo,
(sub '(1 1 1 1) '(1 1))  (1 1)
(1 1)
O que acontece com sua função na chamada abaixo?
(sub '(1) '(1 1 1))
- Uma função
mult,
para multiplicar dois números.
Por exemplo,
(mult '(1 1 1) '(1 1))  (1 1 1 1 1 1)
(1 1 1 1 1 1)
Da mesma forma que podemos definir as operações aritméticas,
podemos também definir os predicados usuais de comparação
numérica.
A função abaixo compara dois números a e b,
e retorna -1 se a < b, 0 se a = b, e 1 se a > b.
(define comp
(lambda (a b)
(cond
((and (zer? a) (zer? b)) 0)
((zer? a) -1)
((zer? b) 1)
(else (comp (dec a) (dec b))))))
Exercício 3.9: Defina as funções abaixo, para operarem sobre dois
naturais dados na representação unária.
Como na definição de soma,
não faça referência a representação por listas;
use apenas as operações sobre números definidas anteriormente.
- Uma função
div,
para dividir dois números,
retornando o quociente da divisão.
Por exemplo,
(div '(1 1 1 1 1) '(1 1))  (1 1)
(1 1)
O que ocorre com sua função se for feita uma divisão por 0?
- Uma função
resto,
retornando o resto da divisão de dois números.
Por exemplo,
(resto '(1 1 1 1 1) '(1 1))  (1)
(1)
Conforme discutimos anteriormente,
um conceito vital em qualquer programa é o da
representação de dados, isto é,
como representar os tipos de dados que o programa manipula usando-se
os mecanismos de representação oferecidos pela linguagem.
Nesta seção, vimos como mesmo tipos básicos,
como números naturais, podem ser representados
através de outros tipos.
Outro ponto importante que devemos ressaltar é o uso de
abstrações nas representações de dados.
O melhor exemplo é dado pela própria linguagem Scheme.
Scheme nos oferece uma representação de números,
junto com operadores de soma, subtração, etc.
Com esses operadores, podemos construir programas usando
números sem nem mesmo saber como esses números são
representados internamente.
Da mesma forma, a linguagem nos oferece listas,
junto com operadores como car, cdr e cons,
e usamos essas listas sem nos preocuparmos em como elas
são implementadas.
Quando definimos uma representação adequada para nossos dados,
devemos sempre escrever as funções necessárias
para manipular essa representação.
Assim, podemos posteriormente usar esse novo tipo sem termos que
nos preocupar em como ele está representado.
3.3 : Tabelas Associativas
Uma outra estrutura de dados muito comum é a tabela,
também chamada de catálogo, diretório,
lista associativa, tabela de símbolos, etc,
conforme seu uso específico.
Esse tipo de estrutura associa um determinado valor,
chamado de chave, a outros valores que tenham alguma
relação específica com a chave.
Um exemplo típico de tabela é um catálogo telefônico,
que associa a cada nome de pessoa (a chave) um ou mais telefones.
Uma maneira de representarmos uma tabela contendo um
`caderno de telefones' é com uma estrutura como mostrada abaixo:
(
(Denise 2221111)
(Paulo 2741555)
(Jose 2221133)
(Maria 2129876)
)
Isso é, uma lista, onde cada elemento da lista é outra lista,
com um nome (a chave) e o telefone associado ao nome.
Exercício 3.10: Usando a representação acima,
faça as tarefas a seguir:
-
Defina uma variável
catalogo,
com sua lista pessoal de telefones.
-
Defina uma função de consulta que receba um nome
e retorne o telefone associado a esse nome em
catalogo.
Por exemplo,
(telefone 'Denise)  2221111
2221111
(dica: use recursão final.)
Da mesma forma que podemos usar funções definidas previamente
na definição de novas funções,
podemos compor tipos para construir tipos mais complexos.
Tendo números, listas, tabelas e conjuntos,
podemos construir conjuntos de tabelas, listas de conjuntos,
e assim por diante.
Exemplo 3.1: Podemos representar o resultado de matrícula de uma faculdade
como uma lista associativa,
que associa o número de matrícula de cada aluno ao conjunto de
disciplinas em que ele se matriculou.
Um exemplo de tal estrutura é mostrado abaixo:
(define M97-1 '(
(M-9611110 (INF1001 FIS1034 MAT1090))
(M-9610222 (FIS1034 FIL1890))
(M-9520000 ())
(M-9523456 (INF1001 FIS1034 MAT1090 JUR1110))))
Exercício 3.11:
Escreva uma função que receba o código de uma disciplina
e uma lista representando um resultado de matrícula,
e retorne uma lista dos alunos matriculados nessa disciplina.
Por exemplo:
(cursando 'MAT1090 M97-1)  (M-9611110 M-9523456)
(M-9611110 M-9523456)
(dica: use suas funções para manipular conjuntos.)
Exercício 3.12: Escreva uma função que receba os números de matrícula de
dois alunos e retorne a lista de disciplinas que ambos fazem
juntos.
(dica: use suas funções para manipular conjuntos e para manipular tabelas.)
Considere agora mais duas tabelas,
uma associando o número de matrícula ao nome do aluno,
e outra associando o código de disciplina ao professor.
Por exemplo:
(define NOMES '(
(M-9611110 "Paulo Moura")
(M-9610222 "Maria Nunes")
(M-9520000 "Marcos Cintra")
(M-9523456 "Marta Silva Teles")))
(define PROFS '(
(INF1001 "Joel Santos Borges")
(FIS1034 "Fabio Tavares")
(MAT1090 "Leila Pinheiro")
(JUR1110 "Sonia Maria do Carmo")
(FIL1890 "Carlos Augusto")))
Exercício 3.13: Defina uma função com a mesma especificação do exercício 3.11,
mas que retorne os nomes dos alunos,
ao invés de seus números de matrícula.
Por exemplo:
(cursando 'MAT1090 M97-1)  ("Paulo Moura" "Marta Silva Teles")
("Paulo Moura" "Marta Silva Teles")
Exercício 3.14: Escreva uma função que receba o nome de um aluno,
e retorne uma lista com os nomes de seus professores.
3.4 : Árvores Binárias
A estrutura apresentada na seção 3.1
para conjuntos pode ser bastante ineficiente para
grandes conjuntos.
Por exemplo, um conjunto com dez mil elementos
exige dez mil comparações para concluirmos que um
elemento não pertence ao conjunto.
Quando consultamos um catálogo telefônico,
não começamos na primeira página e vamos conferindo
cada nome no catálogo até acharmos o que estamos procurando.
A estrutura existente no catálogo,
onde os nomes aparecem em ordem alfabética,
nos permite uma estratégia de busca bem mais eficiente.
Abrimos o catálogo aproximadamente ao meio,
e comparamos os nomes achados com o nome que estamos procurando.
Se o nome que procuramos for `menor'
(isto é, vier antes na ordem alfabética)
que o nome encontrado,
continuamos a busca na primeira metade do catálogo;
se não, procuramos na segunda metade.
A cada passo que damos,
dividimos o espaço de busca ao meio,
até localizarmos a página exata onde o nome que procuramos
se encontra.
Esse algoritmo de busca é conhecido como
busca binária.
Como a cada passo dividimos o número de elementos onde
procurar por dois,
se o número de elementos no início da busca for n,
precisaremos de aproximadamente log 2 n
passos até chegar a 1 elemento,
terminando a busca.
Para dar uma idéia do ganho em eficiência,
em um hipotético catálogo com um milhão de nomes,
precisaríamos de menos de 20 comparações
para achar um dado nome (log2 106 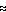 20).
Exercício 3.15: Considere um catálogo de telefones na sua casa:
20).
Exercício 3.15: Considere um catálogo de telefones na sua casa:
- estime, muito aproximadamente,
quantos assinantes estão listados.
- Procure um nome qualquer no catálogo,
e conte quantos outros nomes você tem que ler até achar
(ou não) o que você procura.
- Seria viável achar algum nome no catálogo se este não
estivesse organizado em ordem alfabética?
Poderíamos tentar traduzir diretamente esse algoritmo
para nossa implementação em listas,
mantendo a lista de elementos de um conjunto sempre
em ordem crescente.
Mas existe um problema:
para fazermos a primeira comparação,
precisamos acessar um elemento no meio da lista,
e portanto teríamos que percorrer meia lista;
não há como acessarmos esse elemento diretamente.
Para resolver esse problema,
podemos representar nosso conjunto não como uma lista ordenada,
mas como uma árvore binária de busca.
Para estudarmos árvores de busca,
precisamos saber o que é uma árvore binária.
Uma árvore binária é uma estrutura recursiva,
com uma definição algo similar a que apresentamos para
listas na página lista-rec.
Mais precisamente,
uma árvore binária é ou 1) uma árvore vazia, ou 2) um elemento qualquer, denominado raiz,
mais duas árvores, denominadas sub-árvore esquerda
e sub-árvore direita.
Os elementos de uma árvore são usualmente chamados de nós.
Árvores binárias têm uma representação gráfica
que (em parte) justifica o nome árvore,
mas onde a raiz é representada em cima,
enquanto a árvore `cresce' para baixo.
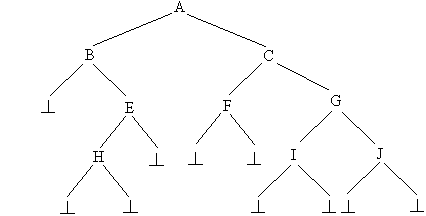
Figura 3.1: Representação gráfica de uma árvore binária
(incluindo as sub-árvores vazias).
A figura 3.1 exemplifica a representação gráfica
de uma árvore binária, onde usamos o símbolo  para representar as árvores vazias.
para representar as árvores vazias.
Figura 3.2: Árvore binária da figura 3.1,
sem mostrar as sub-árvores vazias.
Note que, em geral, não desenhamos as sub-árvores vazias,
donde a mesma árvore poderia ser
desenhada como na figura 3.2.
A raiz dessa árvore é o nó A,
sua sub-árvore esquerda tem B como raiz,
e C é a raiz da sub-árvore direita.
Os nós F, H, I e J são as folhas,
isto é, árvores cujas duas sub-árvores são vazias,
enquanto os nós B e E tem uma das suas
sub-árvores vazias
(a da esquerda em B, e da direita em E).
Os filhos do nó C são os nós F e G;
o nó B tem um único filho, E;
folhas não têm filhos.
O pai do nó E é o nó B;
a raiz é o único nó `órfão' em uma árvore.
A altura de uma árvore é o maior número de nós que
temos que passar para ir da raiz até um nó qualquer da árvore.
Uma árvore vazia tem altura 0, e uma folha tem altura 1.
A árvore da figura 3.2 tem altura 4.
Para manipular árvores binárias em Scheme,
podemos representar essas árvores através de listas.
Uma forma possível para essa representação é
descrita a seguir:
árvores vazias são representadas pela lista vazia.
Árvores não vazias
são representadas por uma lista com 3 elementos:
o primeiro é a raiz da árvore,
enquanto o segundo e o terceiro elementos são listas
representando as sub-árvores esquerda e direita.
Essa representação é chamada pré-fixada.
Exemplo 3.2: Usando a representação pré-fixada
na árvore da figura 3.2, temos a lista
(A (B () (E (H () ()) ())) (C (F () ()) (G (I () ()) (J () ()))))
Ou seja, a raiz da árvore é A,
sua sub-árvore esquerda é a árvore (B () (E (H () ()) ())),
e sua sub-árvore direita é (C (F () ()) (G (I () ()) (J () ()))).
A sub-árvore (B () (E (H () ()) ())) tem como raiz B,
uma árvore vazia como sub-árvore esquerda, e a árvore
(E (H () ()) ()) como sub-árvore direita.
Finalmente, a sub-árvore (C (F () ()) (G (I () ()) (J () ())))
tem raiz C,
sua sub-árvore esquerda é a folha (F () ()),
e sua sub-árvore direita é a árvore (G (I () ()) (J () ())).
Uma forma de melhorarmos essa representação vem do fato que,
usualmente, muitos nós de uma árvore binária são folhas.
Como folhas têm sub-árvores vazias,
não há necessidade de representarmos essas sub-árvores,
desde que haja alguma forma de se saber se uma dada árvore é uma folha.
Por isso, podemos representar folhas diretamente pelo conteúdo de
sua raiz, e utilizar o predicado pré-definido de Scheme list?:
toda árvore cuja representação não for uma lista é uma folha,
e portanto subentende-se que suas sub-árvores são vazias.
Exemplo 3.3:
Com a modificação descrita acima,
a mesma árvore da figura 3.2
pode ser representada pela lista
(A (B () (E H ())) (C F (G I J)))
É importante frizar que folhas não são um caso extra de árvores.
Folhas são árvores `normais', e podem ser representadas dessa forma.
Só na representação de árvores estamos tratando folhas como
um caso a parte, para termos representações mais eficientes.
Exercício 3.16: Desenhe as árvores representadas pelas
seguintes expressões pré-fixadas:
-
(A B C)

(5 (1 3 4) 7)
-
(2 (10 () 3) (2 1 9))
-
A
-
(A () (B () (C () (D () E))))
Da mesma forma que fizemos com nossa representação de números naturais,
vamos definir algumas operações básicas para manipulação de árvores.
Primeiro, definimos uma constante com o valor da árvore vazia;
para testarmos se uma árvore é vazia, definimos o predicado vazia?:
(define arvore-vazia '())
(define vazia? null?)
O predicado folha? verifica se uma árvore é uma folha.
Observe que as folhas são as únicas árvores que não representamos
como listas, portanto basta testar se a representação não é uma
lista para sabermos se é uma folha:
(define folha?
(lambda (a)
(not (list? a))))
Para criarmos uma árvore, dadas suas três partes,
definimos a função cria-arvore:
se as duas sub-árvores e e d forem vazias,
a nova árvore é uma folha, e pode ser representada diretamente
pelo valor da raiz.
Caso contrário, contruimos a lista com os três elementos dados:
(define cria-arvore
(lambda (r e d)
(if (and (vazia? e) (vazia? d))
r
(cons r (cons e (cons d '()))))))
A função raiz retorna a raiz de uma dada árvore:
(define raiz
(lambda (a)
(if (folha? a)
a
(car a))))
Se a árvore é uma folha, seu valor é o valor da raiz.
Caso contrário, a raiz é o primeiro elemento da árvore.
Essa função não pode ser aplicada sobre a árvore vazia,
que não tem raiz.
Exercício 3.17:  Defina as funções
Defina as funções esquerda e direita
para acessar as duas sub-árvores de uma árvore.
Lembre-se de tratar o caso da árvore ser uma folha.
Geralmente, funções recursivas definidas sobre árvores binárias
envolvem duas chamadas recursivas,
uma para cada sub-árvore.
Exemplo 3.4: Considere uma função para contar o número de nós em
uma dada árvore.
Uma árvore vazia tem 0 nós, uma folha tem 1.
Outras árvores tem um nó na raiz,
mais os das suas sub-árvores:
(define num-nos
(lambda (a)
(cond
((vazia? a) 0)
((folha? a) 1) ; caso opcional
(else (+ 1 (num-nos (esquerda a)) (num-nos (direita a)))))))
Na realidade, como os operadores esquerda e direita
já tratam folhas corretamente,
não precisamos tratar folhas de modo separado
(abstração de dados):
(define num-nos
(lambda (a)
(cond
((vazia? a) 0)
(else (+ 1 (num-nos (esquerda a)) (num-nos (direita a)))))))
Com a definição acima,
quando a for uma folha,
(esquerda a) retornará {()},
fazendo (num-nos (esquerda a)) valer 0;
o mesmo vale para o lado direito.
Logo, num-nos retornará 1, como esperado.
Exemplo 3.5:
Uma função para somar 1 em todos os nós de
uma árvore de números pode ser definida como abaixo.
Observe como fazemos a recursão sobre as duas sub-árvores,
e usamos cria-arvore para compor o resultado:
(define soma-arvore
(lambda (a)
(if (vazia? a)
a
(cria-arvore (+ 1 (raiz a))
(soma-arvore (esquerda a))
(soma-arvore (direita a))))))
Exercício 3.18: Usando as operações definidas acima para
manipulação de árvores,
escreva as funções abaixo:
- uma função que retorne a soma de todos os nós de
uma dada árvore de números;
- uma função que retorne a altura de uma dada árvore;
(dica: use a função pré-definida
max.)
- uma função que retorne uma lista com todos os elementos
de uma dada árvore;
(dica: use a função pré-definida
append,
ou a função definida no exercício 2.2.h,
para juntar as várias partes do resultado.)
- na função do item anterior,
em que ordem os elementos da árvore aparecem na lista?
Qual é o primeiro? Qual é o último?
-
uma função que receba n e retorne uma árvore contendo
n nós, todos com o valor 1.
Procure fazer as duas sub-árvores terem sempre aproximadamente
o mesmo número de elementos.
- uma função que receba n e retorne uma árvore contendo
n nós, cada um com um valor diferente de 1 até n.
Procure fazer as duas sub-árvores terem sempre aproximadamente
o mesmo número de elementos.
(dica: defina sua função com dois parâmetros, i e n,
para retornar uma árvore numerada de i até n.)
Exercício 3.19: Considere a função definida no exercício 3.18.e.
Qual é a relação entre o n dado e a altura da árvore resultante
dessa função?
Representação de Expressões Aritméticas
Um uso bastante comum de árvores binárias é
na representação de expressões aritméticas.
Essas árvores têm como elementos números e
operadores aritméticos.
Toda árvore cuja raiz é um número é uma folha.
Quando a raiz é um operador,
as sub-árvores esquerda e direita representam o primeiro e
o segundo operandos,
respectivamente.
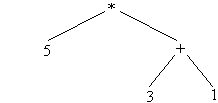
Figura 3.3: Árvore binária representando a expressão 5 × (3 + 1).
Exemplo 3.6: A figura 3.3
mostra a árvore binária que representa
a expressão 5 × (3 + 1).
Essa árvore tem como raiz o nó *,
como sub-árvore esquerda uma folha com raiz 5,
e como sub-árvore direita outra expressão.
Essa sub-árvore direita, por sua vez,
tem como raiz o +,
como sub-árvore esquerda o 3,
e como sub-árvore direita o 1.
Exercício 3.20: Desenhe árvores representando as seguintes
expressões:
- 3+4
- 3 × 4 + 5
- 3 + 4 × 5
 3+4+5
3+4+5
- 3/4 + 5/2
- 3+2+10+9+2
- (3+2)+10+(9+2)
Se aplicarmos a representação pré-fixada descrita acima
sobre árvores de expressões,
vamos chegar exatamente na forma como escrevemos
expressões aritméticas em Scheme.
Por exemplo,
a árvore na figura 3.3
é representada pela lista
(* 5 (+ 3 1)),
que é como representamos aquela expressão em Scheme.
Como já vimos, uma árvore binária não vazia é composta
por três partes:
a raiz, a sub-árvore esquerda e a sub-árvore direita.
Na representação pré-fixada, colocamos esses três elementos em uma lista,
na ordem raiz -- sub-árvore esquerda -- sub-árvore direita,
mas poderíamos colocá-los em qualquer ordem.
Em particular,
na chamada notação in-fixada,
colocamos primeiro a sub-árvore esquerda
(representada na ordem in-fixada também),
em seguida a raiz, e finalmente a sub-árvore direita
(também na ordem in-fixada).
Na notação pós-fixada, por sua vez,
colocamos primeiro a sub-árvore esquerda
(representada agora na ordem pós-fixada),
em seguida a sub-árvore direita (também na ordem pós-fixada),
e no final a raiz.
Exemplo 3.7: Voltando à figura 3.3,
temos que a representação in-fixada daquela expressão
é bastante familiar: (5 * (3 + 1)).
A representação pós-fixada, por sua vez, é (5 (3 1 +) *).
Exercício 3.21: Represente as árvores desenhadas no exercício 3.20
nas formas in-fixada e pós-fixada.
É interessante observar como a representação que usamos
para árvores, in-fixada, pré-fixada ou pós-fixada,
fica `abstraida' quando usamos nossas funções de manipulação
raiz, folha?, cria-arvore, etc.
Por exemplo, a função soma-arvore descrita no exemplo 3.5
não faz nenhuma referência ao fato da árvore estar representada
na forma pós-fixada.
Se decidirmos usar a representação pós-fixada, por exemplo,
precisamos apenas redefinir nossas operações básicas.
Exercício 3.22: Redefina as funções básicas sobre árvores
(arvore-vazia, vazia?, folha, raiz,
direita, esquerda e cria-arvore)
para operarem sobre árvores representadas na forma in-fixada.
Note que nem todas precisam ser modificadas.
Exercício 3.23: Escreva uma função que receba uma expressão na forma
pré-fixada e retorne a representação da mesma expressão
na forma in-fixada.
Por exemplo
(converte '(* (+ 5 4) (- 2 3)))  ((5 + 4) * (2 - 3))
((5 + 4) * (2 - 3))
(dica: se sua árvore é uma folha (isto é, um número),
é fácil, pois folhas são iguais nas formas pré-fixada e in-fixada.
Caso contrário, troque os elementos de ordem,
chamando a função recursivamente para converter
as sub-árvores.)
Árvores Binárias de Busca
Vamos voltar ao nosso problema de procurar
um valor em um determinado conjunto de maneira eficiente,
e ver como podemos usar árvores binárias
para resolvê-lo usando listas.
Imagine uma árvore binária de números,
com a seguinte propriedade:
todos os elementos da sub-árvore esquerda são
menores que a raiz,
e todos os elementos da sub-árvore direita são
maiores que a raiz.
Se formos procurar um determinado valor nessa árvore,
apenas comparando nosso valor com a raiz,
sabemos em que sub-árvore nosso valor pode ser encontrado:
se o valor for igual à raiz, encontramos o que estamos procurando;
se for menor, só pode estar na sub-árvore esquerda,
e se for maior, na sub-árvore direita.
Assim, com apenas uma comparação, dividimos em duas a
árvore onde precisamos continuar a busca.
Se as sub-árvores também tiverem a propriedade acima,
podemos continuar nossa busca `descendo' pela árvore,
em cada passo decidindo se continuamos pela esquerda ou
pela direita, até encontrarmos o elemento procurado ou
chegarmos em uma árvore vazia (significando que o elemento
não se encontra em nosso conjunto).
Mais precisamente,
definimos uma árvore binária de busca,
ou simplesmente árvore de busca,
como uma árvore binária onde todas as sub-árvores
satisfazem o invariante:
se a árvore não é vazia,
todos os elementos da sub-árvore esquerda são menores que a raiz,
e todos os elementos da sub-árvore direita são maiores que a raiz.
Exemplo 3.8:
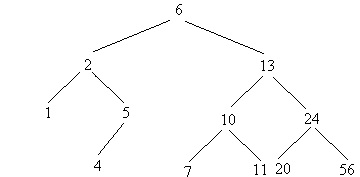
Figura 3.4: Uma árvore de busca.
A árvore na figura 3.4 ilustra uma
possível árvore de busca para o conjunto
{1,2,4,5,6,7,10,11,13,20,24,56}.
Exercício 3.24: Um mesmo conjunto pode ser representado por diversas
árvores de busca.
Desenhe duas outras árvores de busca que representem o mesmo
conjunto da árvore da figura 3.4.
Exercício 3.25:  Defina uma função que retorne o menor elemento de
uma árvore de busca.
(dica: o menor elemento de uma árvore de busca está sempre no
seu `canto' mais esquerdo.)
Exercício 3.26: Escreva o predicado
Defina uma função que retorne o menor elemento de
uma árvore de busca.
(dica: o menor elemento de uma árvore de busca está sempre no
seu `canto' mais esquerdo.)
Exercício 3.26: Escreva o predicado pertence? sobre árvores de busca.
Lembre-se: se a árvore for vazia, nenhum elemento pertence a ela.
Caso contrário,
se o elemento procurado for igual à raiz, então ele pertence ao conjunto.
Se ele for menor que a raiz, deve-se procurar na sub-árvore esquerda;
se for maior, na sub-árvore direita.
Exercício 3.27:  Escreva um predicado para inserir um novo elemento em uma
dada árvore de busca.
Se a árvore for vazia, retorne uma folha com o novo elemento.
Se o elemento a ser inserido for igual à raiz,
então ele já pertence a árvore,
e podemos retornar a árvore sem modificações.
Se ele for menor que a raiz, devemos inserí-lo na sub-árvore esquerda;
se for maior, na sub-árvore direita.
Antes de continuarmos, é importante frizar o que vimos nesta seção:
como diferentes representações para um mesmo tipo,
como listas × árvores de busca para conjuntos,
podem implicar em operações com desempenhos bastante desiguais.
Não por acaso, em geral representações com operações mais eficientes
envolvem implementações mais complexas.
O estudo de representações eficientes para diferentes tipos
de informação é uma das áreas centrais em computação.
Na próxima seção,
vamos ver uma outra representação para números naturais,
bem mais eficiente que a que vimos na seção 3.2.
Escreva um predicado para inserir um novo elemento em uma
dada árvore de busca.
Se a árvore for vazia, retorne uma folha com o novo elemento.
Se o elemento a ser inserido for igual à raiz,
então ele já pertence a árvore,
e podemos retornar a árvore sem modificações.
Se ele for menor que a raiz, devemos inserí-lo na sub-árvore esquerda;
se for maior, na sub-árvore direita.
Antes de continuarmos, é importante frizar o que vimos nesta seção:
como diferentes representações para um mesmo tipo,
como listas × árvores de busca para conjuntos,
podem implicar em operações com desempenhos bastante desiguais.
Não por acaso, em geral representações com operações mais eficientes
envolvem implementações mais complexas.
O estudo de representações eficientes para diferentes tipos
de informação é uma das áreas centrais em computação.
Na próxima seção,
vamos ver uma outra representação para números naturais,
bem mais eficiente que a que vimos na seção 3.2.
3.5 : Notação Posicional e Bases de Numeração
A notação unária, vista na seção 3.2,
apesar de muito simples, não é muito eficiente.
Por exemplo, para representarmos o número 1.598.980,
precisaremos de uma lista com 1.598.980 elementos.
Para calcularmos uma soma como 1354+4590 iremos executar
milhares de vezes as funções dec e inc.
Uma representação bem mais eficiente para números naturais,
que podemos usar no computador,
é a que a humanidade já vem usando há alguns séculos:
a notação posicional decimal, ou base 10.
Usando a notação decimal,
podemos representar um número como uma lista de dígitos,
cada um entre 0 e 9, onde cada casa vale 10 vezes mais que
a anterior.
Por convenção, vamos armazenar a lista começando com as unidades,
depois as dezenas, e assim por diante.
Isso é, um número como 1.542 será representado pela lista
(2 4 5 1).
Assim, ao invés de uma lista com 1.542 elementos da notação unária,
temos agora uma lista com apenas 4 elementos.
É comum acharmos anti-natural essa
representação aparentemente invertida,
com as unidades à esquerda.
Entretanto, se pensarmos em como fazemos operações aritméticas,
vamos perceber que em geral tratamos os vários dígitos
nessa ordem.
Por exemplo, quando somamos dois números,
primeiro somamos as unidades, depois as dezenas,
e assim por diante.
Por isso, essa ordem torna mais simples a implementação
de várias operações sobre números.
Para facilitar nossas operações,
vamos convencionar que nossos números nunca
terão zeros não significativos,
isto é, o último elemento da lista nunca será 0.
(Temos aqui mais um exemplo do uso de um invariante).
Em particular, o número 0 será representado pela lista vazia,
e não pela lista (0).
Para entender melhor a representação base 10,
considere a função base->num definida abaixo.
Essa função recebe um número na notação base 10 e o converte
para um número na representação interna de Scheme.
(define base->num
(lambda (l)
(if (null? l)
0
(+ (car l) (* base (base->num (cdr l)))))))
onde base foi definida como
(define base 10)
Ao calcularmos o valor de (base->num '(1 8 5))
teremos o traço abaixo:
(base->num '(1 8 5))

(+ 1 (* 10 (base->num '(8 5))))

(+ 1 (* 10 (+ 8 (* 10 (base->num '(5))))))

(+ 1 (* 10 (+ 8 (* 10 (+ 5 (* 10 (base->num '())))))))

(+ 1 (* 10 (+ 8 (* 10 (+ 5 (* 10 0))))))

(+ 1 (* 10 (+ 8 (* 10 5))))

(+ 1 (* 10 58))

581 
A função inversa,
que converte da representação interna de Scheme para nossa base 10,
pode ser definida como:
(define num->base
(lambda (n)
(if (zero? n)
'()
(cons (remainder n base) (num->base (quotient n base))))))
Como exemplo, o traço de (num->base 581) será:
(num->base 581)

(cons (remainder 581 10) (num->base (quotient 581 10)))

(cons 1 (num->base 58))

(cons 1 (cons (remainder 58 10) (num->base (quotient 58 10))))

(cons 1 (cons 8 (num->base 5)))

(cons 1 (cons 8 (cons (remainder 5 10) (num->base (quotient 5 10)))))

(cons 1 (cons 8 (cons 5 (num->base 0))))

(cons 1 (cons 8 (cons 5 '())))

'(1 8 5) 
Operações Aritméticas com Notação Posicional
Vamos ver agora como definir as operações aritméticas
usando essa representação.
A constante zero é trivialmente definida como
(define zero '())
e o predicado zer? como
(define zer? null?)
Note como o invariante simplifica esse predicado.
Se não tivessemos o invariante,
teríamos que verificar casos como (0 0 0).
A operação de incremento já não é tão simples.
Temos três casos:
se a lista for vazia (isto é, zero),
o incremento é '(1).
Se a lista não for vazia,
verificamos se podemos incrementar seu primeiro dígito.
Se sim, isso é tudo que precisamos fazer.
Mas se ao incrementarmos o primeiro dígito chegamos na base,
temos que usar o `vai um':
o primeiro dígito vai para 0 e incrementamos o resto da lista.
Traduzindo para Scheme temos13 :
(define inc
(lambda (n)
(cond
((null? n) '(1))
((= (+ (car n) 1) base) (cons 0 (inc (cdr n)))))))
(else (cons (+ (car n) 1) (cdr n)))
Exercício 3.28: Faça o traço das chamadas (inc '(9 3 1)) e
(inc '(9 9)).
Exercício 3.29: Defina a função dec para decrementar um número
representado na base 10.
Tendo definido as operações primitivas
zero, zer?, inc e dec,
podemos definir a operação de soma exatamente como havíamos
definido na representação unária.
Apesar de correta, essa operação seria tão ineficiente
quanto era no caso anterior.
Nos valendo da representação base 10,
podemos definir a função de soma de uma forma um pouco
mais complexa, mas muito mais eficiente.
Novamente, vamos imitar o que a humanidade faz
há alguns séculos.
Vamos imaginar que queremos somar 98+1707:
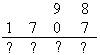 Para executarmos essa soma,
primeiro somamos os dois primeiros algarismos;
caso essa soma seja maior que 10 (a base),
diminuimos 10 do total e marcamos um `vai um'.
Para executarmos essa soma,
primeiro somamos os dois primeiros algarismos;
caso essa soma seja maior que 10 (a base),
diminuimos 10 do total e marcamos um `vai um'.
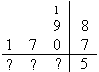 A seguir, repetimos exatamente os mesmos passos
para o resto dos dois números
(lidos da direita para a esquerda).
Isso é, somamos os dois primeiros algarismos e o `vai um',
verificamos se o resultado é maior que a base, etc.
Esse processo deve ser repetido até os dois números terminarem.
Porém, ocorre frequentemente de um dos números terminar antes
do outro.
No nosso exemplo, vamos chegar na seguinte situação:
A seguir, repetimos exatamente os mesmos passos
para o resto dos dois números
(lidos da direita para a esquerda).
Isso é, somamos os dois primeiros algarismos e o `vai um',
verificamos se o resultado é maior que a base, etc.
Esse processo deve ser repetido até os dois números terminarem.
Porém, ocorre frequentemente de um dos números terminar antes
do outro.
No nosso exemplo, vamos chegar na seguinte situação:
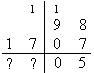 Nesse caso, simplesmente estendemos o número menor com um 0
e continuamos o processo:
Nesse caso, simplesmente estendemos o número menor com um 0
e continuamos o processo:
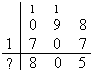 Quando finalmente os dois números terminarem,
chegamos ao fim da nossa operação:
Quando finalmente os dois números terminarem,
chegamos ao fim da nossa operação:
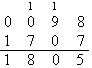 Note que, se os dois números a serem somados respeitarem o invariante
(isto é, se eles não tiverem zeros à esquerda),
o resultado também respeitará.
Note que, se os dois números a serem somados respeitarem o invariante
(isto é, se eles não tiverem zeros à esquerda),
o resultado também respeitará.
(define soma
(lambda (a b v) ; v indica "vai um"
(cond
((and (null? a) (null? b)) (if (zero? v) '() '(1)))
((null? a) (soma '(0) b v))
((null? b) (soma a '(0) v))
(else (let ((d (+ (car a) (car b) v)))
(if (< d base)
(cons d (soma (cdr a) (cdr b) 0))
(cons (- d base) (soma (cdr a) (cdr b) 1))))))))
Figura 3.5: Função para somar dois números na base decimal.
A tradução para Scheme do algoritmo descrito acima
está na figura 3.5.
Vários pontos merecem comentário.
Primeiro, nossa função deve ter 3 argumentos:
os dois números sendo somados, e o `vai um'.
Quando os dois números terminarem,
basta verificarmos o `vai um' para termos o resultado.
Se um dos números terminar antes do outro,
chamamos recursivamente a função com os mesmos argumentos,
mas trocando o número que terminou pela lista (0).
Com isso, temos o mesmo efeito de estendermos o número com zeros.
Finalmente, no caso normal,
definimos uma variável local d
com a soma dos dois primeiros algarismos e o vai um.
Dependendo desse valor ser menor que a base (10) ou não,
a chamada recursiva deve indicar (ou não) o vai um.
Exercício 3.30: Qual o traço da chamada (soma '(8 9) '(7 0 7 1))?
Exercício 3.31:  Implemente as seguintes funções,
para operarem sobre dois números representados na base 10:
Implemente as seguintes funções,
para operarem sobre dois números representados na base 10:
- uma função para subtrair dois números.
Siga o mesmo raciocínio que usamos para
soma,
tentando traduzir para Scheme o algoritmo de subtração que
usamos manualmente.
- Um predicado para testar se um número é menor que outro.
Base Binária
Se redefinirmos a variável base como 1,
teremos problemas já na função num->base;
como (quotient n 1) é igual a n,
essa função ficaria em loop se a base fosse 1.
Mas se redefinirmos base como qualquer outro número
natural maior ou igual a 2,
todas as funções continuarão funcionando corretamente.
A maneira mais fácil de percebermos isso é verificando
que em nenhuma das funções usamos o fato de base ser 10.
Também é importante observarmos que, para qualquer número natural n,
(base->num (num->base n))  n
n
Isso significa que o resultado de (num->base n) continua sendo
uma boa representação para um número natural n qualquer,
mesmo com outras bases,
pois sempre podemos voltar ao número original usando base->num.
Para verificarmos que isso é realmente verdade,
podemos usar indução.
Se n=0, a igualdade é trivial, pois:
(base->num (num->base 0))
 definição de
definição de num->base
(base->num '())
 definição de
definição de base->num
0 
Para outros valores de n, com base sendo um natural b>=2,
temos:
(base->num (num->base n))
 def.
def. num->base
(base->num (cons n mod b (num->base (n÷ b))))
 def.
def. base->num
(+ n mod b (* b (base->num (num->base (n÷ b)))))
 indução
indução
(+ n mod b (* b (n÷ b)))

n mod b + b × (n÷ b)
 aritmética
aritmética
n 
Note que, no caso específico de base=1,
a função num->base não termina,
e portanto a prova acima não é válida.
De particular interesse para nós é a base 2,
chamada de base binária.
Nessa base, qualquer número pode ser escrito usando-se
apenas os algarismos 0 e 1;
por exemplo, o número 154 pode ser representado em binário pela
lista '(0 1 0 1 1 0 0 1), pois:
0 + (2 × (1 + 2 × (0 + 2 × (1 + 2 × (1 + 2 × (0
+ 2 × (0 + 2 × 1))))))) = 154
Apesar da representação de um número na base binária
usar mais algarismos que na base decimal,
a representação e manipulação de cada algarismo é bem mais simples
na base binária, pois só existem dois algarismos possíveis.
A base binária é a forma usual como um computador
representa números internamente.
Entretanto, através do uso de mecanismos de abstração,
raramente essa representação é visível quando utilizamos um
computador:
operações como + e * têm comportamento igual
em qualquer representação,
e o uso de funções como num->base e base->num
permite que números sejam lidos e escritos externamente
na base decimal, com a qual estamos acostumados.
Exercício 3.32: Converta os números abaixo para as bases indicadas
(se quiser, use sua função num->base,
definindo antes base com o valor adequado):
- 2, 4, 6, 16, e 33 para a base binária (base 2);
- 3, 6, e 12 para a base 3;
- 13, 64, e 60 para a base 16.
Exercício 3.33: Converta os números em base binária
'(0 1 1 0 1), '(1 1 1), e
'(1 1 0 1) para a base decimal
(se quiser, use a função base->num,
definindo antes base com o valor 2).
Exercício 3.34: Faça o traço da chamada
(soma '(1 1 1 0 1) '(0 1 1))
assumindo que base vale 2.
Converta os argumentos para a base decimal
e verifique o resultado.
Exercício 3.35: Se um número precisa de x dígitos para ser
representado na base decimal,
quantos dígitos serão necessários para representá-lo
na base binária?
Exercício 3.36: Da mesma forma que é muito simples multiplicarmos
um número por 10, quando usamos nossa notação decimal,
algumas operações sobre números na base binária tem
implementações triviais.
Mostre como executar as seguintes operações
sobre um dado número representado na base binária:
- dup2(x) = 2x
- div2(x) = x ÷ 2
- verificar se o número é par.
Exercício 3.37: Considere as seguintes igualdades:
a × b = 0, para b=0;
a × b = 2(a × (b÷ 2)), para b par;
e a × b = a+2(a × (b÷ 2)), para b ímpar
(note que, para b ímpar, b÷ 2 = (b-1)÷ 2).
Usando essas igualdades,
e as funções já definidas nos exercícios anteriores,
implemente uma função para multiplicar dois
números na base binária.
(É interessante observar que esse algoritmo de multiplicação é
exatamente o mesmo que usamos para multiplicar dois números
manualmente, `traduzido' para a base binária.
Nesta base, o algoritmo fica bastante simplificado,
pois a multiplicação por cada algarismo é trivial,
sendo sempre uma multiplicação por 0 ou por 1.)
(dica: veja o exercício 2.12.)
3.6 : Outros Exercícios
Exercício 3.38: Podemos representar um polinômio
an xn + an-1 xn-1 + ... + a1 x + a0
no computador através da lista de seus coeficientes,
(a0 a1 ... an).
Por exemplo, o polinômio 3x2 - 5x + 23 é representado pela
lista (23 -5 3).
-
Usando esta representação, escreva uma função que receba um polinômio
e um valor para x, e retorne o valor do polinômio para o x dado.
(dica: use a igualdade
an xn + an-1 xn-1 + ... + a1 x + a0 =
a0 + x(a1 + x(a2 + ... + x (an) ... ))
para simplificar os cálculos.)
- Escreva uma função auxiliar que receba n e retorne a lista
(1/1! - 1/3! 1/5! - 1/7! ... )
com n elementos.
-
A lista gerada pelo item anterior, com n=4, representa o polinômio
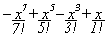 Usando a função do primeiro item,
calcule o valor desse polinômio para alguns valores de x entre 0 e 1.
Compare os valores obtidos com os de sin x.
Aumente o número de termos do seu polinômio
(aumentando n na função do item anterior),
e repita a comparação.
Usando a função do primeiro item,
calcule o valor desse polinômio para alguns valores de x entre 0 e 1.
Compare os valores obtidos com os de sin x.
Aumente o número de termos do seu polinômio
(aumentando n na função do item anterior),
e repita a comparação.
-
Escreva uma função que some dois polinômios.
A soma de dois polinômios é um polinômio de grau igual ao
maior grau entre os polinômios somados,
e onde cada coeficiente é igual a soma dos coeficientes
de igual grau nos polinômios somados.
(dica: veja exercício 2.5.f.)
-
Escreva uma função que receba um polinômio e retorne sua derivada.
Relembrando, a derivada de um polinômio de grau n
an xn + an-1 xn-1 + ... + a1 x + a0
é o polinômio de grau n-1
(n × an) xn-1 +
((n-1) × an-1) xn-2
+ ... + 2a2 x + a1
(define calc
(lambda (exp)
(cond
((number? exp) exp)
((equal? (car exp) '+) (+ (calc (cadr exp)) (calc (caddr exp))))
((equal? (car exp) '*) (* (calc (cadr exp)) (calc (caddr exp)))))))
Figura 3.6: Definição inicial da função calc.
Exercício 3.39:  Considere a função mostrada na figura 3.6,
onde
Considere a função mostrada na figura 3.6,
onde number? é um predicado pré-definido que testa se
um determinado valor é um número.
- faça o traço da chamada
(calc '(+ (* 4 5) 2)).
- Modifique a função
calc de forma que ela também
interprete subtração e divisão.
- Modifique sua função para tratar expressões com nomes,
como por exemplo
(+ x y).
Para isso,
vamos precisar de um ambiente,
que associe cada nome ao seu valor.
Esse ambiente pode ser representado como uma lista associativa;
por exemplo, o ambiente {x 12,
12, y 23}
será representado pela lista
23}
será representado pela lista ((x 12) (y 23)).
O ambiente deve então ser passado como um parâmetro adicional
para a função calc,
e consultado (use uma função auxiliar consulta) toda
vez que a expressão for um nome
(use o predicado symbol? para testar se a expressão é um nome).
Um exemplo de uso segue abaixo;
lembre-se que calc agora recebe dois argumentos,
a expressão a ser calculada e o ambiente com o valor das variáveis:
(calc 'b '((a 1) (b 8)))  8
8
(calc '(* (+ y 3) x) '((x 2) (y 5)))  16
16
- Usando a função acima,
escreva uma função
declare que acrescente um
par (nome valor) em um dado ambiente,
mas onde o valor pode ser dado através de uma expressão.
Essa função recebe um par (nome expressão) e um ambiente,
e retorna o novo ambiente.
Por exemplo:
(declare '(x 1) '((y 2) (z 5)))  ((x 1) (y 2) (z 5))
((x 1) (y 2) (z 5))
(declare '(val (* 2 2)) '((y 2) (z 5)))  ((val 4) (y 2) (z 5))
((val 4) (y 2) (z 5))
(declare '(x (+ 4 y)) '((y 2) (z 5)))  ((x 6) (y 2) (z 5))
((x 6) (y 2) (z 5))
- Usando a função acima,
acrescente na sua função
calc uma operação para definir
valores (parecida com o let), chamada def.
O uso de def é exemplificado abaixo:
(calc '(def (x 10) (+ x 3)) '())  13
13
(calc '(def (x (+ 2 8)) (* (+ x 3) y)) '((y 5)))  65
65
(dica: use calc para calcular o valor da expressão,
em um ambiente onde a nova variável foi associada ao valor adequado.
Use a função do item anterior para construir esse novo ambiente.)
Capítulo 4 :
Programação Procedural
Até agora,
temos trabalhado primordialmente com avaliação de expressões:
entramos com uma expressão para o interpretador,
e este mostra o valor final da expressão.
Após o término da execução de uma expressão,
tudo que sobra é seu valor na tela;
de resto, o sistema não sofre qualquer modificação.
Existem outros tipos de operações,
como o define, que,
ao contrário de apenas calcular um valor,
alteram o estado do sistema,
afetando a maneira como esse funciona.
Quando executamos um define,
não estamos interessados no valor retornado,
e sim na alteração causada no ambiente pela
associação de um símbolo com um valor.
Esse tipo de operação é chamado de procedimento.14
Em geral,
usamos o termo procedimento
para nos referir a uma função quando queremos frizar o
fato dela ser usada para alterar o ambiente,
e não para retornar um valor.
Ao contrário, quando quisermos frizar
que uma função não é um procedimento,
podemos chamá-la de função pura.
Assim, procedimentos são funções que, quando chamadas,
modificam o ambiente de alguma forma,
enquanto funções puras simplesmente retornam um resultado.
A programação com procedimentos
nos leva a um estilo de programação um pouco diferente,
usualmente chamado programação procedural,
ou programação imperativa,
em oposição ao estilo que vinhamos adotando até então,
chamado programação funcional.
Em especial,
o uso de traços não é suficiente para descrevermos
o funcionamento de procedimentos,
pois não temos como expressar as modificações no ambiente.
Recursão continua sendo um recurso fundamental em
programação procedural,
mas como nunca utilizamos valores retornados por procedimentos,
procedimentos quase sempre usarão apenas recursão final.
4.1 : Interação
Todas as funções que definimos até agora recebem argumentos e
retornam um valor.
Através do interpretador Scheme,
podemos chamar qualquer função fornecendo seus argumentos,
e ver o seu resultado.
Entretanto, muitos programas tem outras formas
de interação com o usuário.
Muitas vezes é necessário mostrar resultados intermediários,
ler outros dados fornecidos pelo usuário,
ou apenas mostrar os resultados em algum outro formato.
Para isso,
as linguagens oferecem funções especiais
tanto para entrada quanto para a saída de dados.
Para ilustrar nossa discussão,
vamos imaginar que queremos uma função que,
quando chamada com um argumento x,
mostre algo como
O valor do seno de x é y
onde y é o valor de sin x.
Essa função (ou, mais especificamente, procedimento)
poderia ser escrita como:
(define mostra-seno
(lambda (x)
(begin (display "O valor do seno de ")
(display x)
(display " é ")
(display (sin x)))))
Para mostrarmos um valor na tela,
usamos o procedimento display,
que simplesmente mostra na tela o valor de
seu único argumento.
Note que cada chamada à função display
exibe uma parte do nosso resultado na tela;
o valor retornado pela função é totalmente irrelevante para nós.
Para agrupar essas chamadas,
usamos o construtor begin:
uma chamada (begin c1 c2 ... cn)
executa c1, depois c2, etc,
e finalmente retorna o resultado de cn.
Os valores retornados por c1,c2,...,cn-1
são simplesmente descartados.15
É interessante observar que o construtor begin
só faz sentido junto com procedimentos.
Uma expressão como
(begin (* 10 5) (- 5 4))  1
1
apesar de correta para o interpretador,
é um pouco absurda,
pois vai calcular (* 10 5)
para jogar fora o resultado.
Vamos ver agora um exemplo um pouco mais complexo.
Exemplo 4.1:
Imagine que queremos mostrar todos os elementos de uma
dada lista, um por linha.
No caso base, que é a lista vazia,
simplesmente não fazemos nada,
pois não há nada a ser mostrado.
No caso recursivo,
mostramos o primeiro elemento e chamamos o procedimento
recursivamente para mostrar o resto da lista:
(define mostra-lista
(lambda (l)
(if (null? l)
'()
(begin
(display (car l))
(newline)
(mostra-lista (cdr l))))))
O procedimento newline é um procedimento sem parâmetros,
que quando chamado pula uma linha no terminal.
A lista vazia no primeiro caso do if é algo artificial,
pois esse é o caso em que não há nada a ser feito.
Da mesma forma que colocamos '(),
poderíamos ter colocado 0, ou mesmo 1.
Como essa situação ocorre frequentemente em procedimentos,
existe um formato especial para isso:
o segundo caso do if é opcional,
e quando não fornecido significa exatamente que não há nada
a ser feito nem valor a ser dado neste caso.
Portanto, nosso exemplo pode ser reescrito assim,
usando-se not na condição para invertermos os casos:
(define mostra-lista
(lambda (l)
(if (not (null? l))
(begin
(display (car l))
(newline)
(mostra-lista (cdr l))))))
Esse uso do if com apenas um caso é outra característica
típica de programação procedural.
Em funções puras sempre precisamos especificar o valor a ser
retornando, nos dois casos de um condicional.
Em procedimentos, é comum não haver nada a ser retornado nem
executado em um dos casos, então podemos simplesmente omitir esse caso.
Exemplo 4.2:
Um procedimento bastante útil é um que mostra repetidas vezes um
mesmo texto na tela.
Sua definição é bastante simples:
(define (mostra-n n t)
(if (not (zero? n))
(begin
(display t)
(mostra-n (- n 1) t))))
Com essa função, uma chamada como (mostra-n 40 "*") produz
40 asteriscos na saída,
e uma chamada como (mostra-n x " ") serve para
pular x espaços em branco.
Exercício 4.1:
Escreva procedimentos para realizar as tarefas abaixo:
-
Dado um número n,
escrever os valores de n2,(n-1)2,...,9,4,1,
um por linha.
-
Dado um número n,
escrever os valores de 1, 4, 9, ...,(n-1)2,n2,
um por linha.
-
Escrever os elementos de uma dada lista, um por linha,
precedidos pelo seu número de ordem.
Por exemplo, uma chamada como
(mostra-num-linha '(martelo prego alicate))
deve produzir uma saída como
1 - martelo
2 - prego
3 - alicate
 Escrever os elementos de uma dada lista, dois por linha,
separados por um espaço.
Por exemplo, uma chamada como
Escrever os elementos de uma dada lista, dois por linha,
separados por um espaço.
Por exemplo, uma chamada como
(mostra-lista '(martelo prego alicate tesoura serrote))
deve produzir uma saída como
martelo prego
alicate tesoura
serrote
(dica: use o predicado even? para decidir se é hora
de mudar de linha.)
- Generalize a função do exercício anterior para,
ao invés de escrever dois elementos por linha,
escrever n por linha, onde n é um parâmetro do procedimento.
Repetições em Programação Procedural
Conforme já mencionamos,
o estilo de programação procedural nos leva
a usar com bastante frequência procedimentos
com recursão final.
Portanto, é bastante natural usarmos o do
na programação de procedimentos.
Analisando a estrutura das chamadas recursivas em procedimentos,
podemos perceber que é bastante comum a chamada recursiva ser
precedida por outras ações, dentro de uma construção begin.
O do tem uma facilidade específica para estruturarmos
essas ações, no chamado corpo do do.
O corpo de um do são expressões opcionais que podemos escrever
depois das variáveis, condição de parada e valor final.
As ações especificadas nesse corpo são executadas a cada repetição.
A sintaxe geral da construção do,
incluindo um corpo opcional, é mostrada abaixo:
(do ([n1 v1 e1]
...
[nn vn en])
(teste valor-final)
corpo)
A sintaxe geral de do mostrada acima é equivalente a:
(define aux
(lambda (n1 ... nn)
(if teste
valor-final
(begin
corpo
(aux e1 ... en)))))
(aux v1 ... vn) ; <= expressao equivalente ao do
A única diferença para o formato do do com que vinhamos
trabalhando é a presença do corpo.
Este pode ser formado por um número qualquer de expressões,
sem necessidade de um begin,
que são executadas a cada repetição do do.
Exemplo 4.3: Um procedimento para mostrar todos os valores de uma dada lista,
um por linha, é mostrado a seguir:
(define mostra
(lambda (l)
(do ((l1 l (cdr l1)))
((null? l1))
(display (car l1))
(newline))))
Observe que o segundo argumento do do,
a lista ((null? l1)),
tem um único elemento, o teste (null? l1).
Como mostra é um procedimento, não precisamos
especificar qual será o valor final do do.
Neste exemplo, o corpo do do é formado por duas
expressões, (display (car l1)) e (newline).
Para cada valor de l1 dentro da repetição,
essas duas expressões são executadas.
Observe que não precisamos usar begin para juntar
vários comandos no corpo do do.
Exercício 4.2: Reescreva os procedimentos do exercício 4.1
usando do.
Exercício 4.3: Através de procedimentos adequados,
diversos tipos de dados representados por listas podem
ser mostrados de forma mais natural.
Defina procedimentos para exibir os tipos abaixo,
no formato mostrado:
 Conjuntos representados por listas.
Mostre os elementos entre chaves
Conjuntos representados por listas.
Mostre os elementos entre chaves {...},
separados por vírgulas;
por exemplo:
(mostra-conjunto '(3 10 9 5))  {3,10,9,5}
{3,10,9,5}
-
Números na representação binária.
Mostre os números com os dígitos mais significativos à esquerda,
e seguidos por um
b.
Trate o valor zero de maneira adequada;
por exemplo:
(mostra-binario '(0 0 1 0 1))  10100b
10100b
(mostra-binario '())  0b
0b
-
Catálogos representados por listas associativas.
Mostre cada par chave
 valor em uma linha,
com um
valor em uma linha,
com um -> entre eles;
por exemplo:
(mostra-catalogo '((Denise 2221111) (Paulo 2741555)))

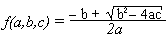
 Conjuntos representados por árvores de busca.
Mostre os elementos entre chaves
Conjuntos representados por árvores de busca.
Mostre os elementos entre chaves {...},
separados por vírgulas, em ordem crescente;
por exemplo:
(mostra-conjunto '(5 (3 1 4) (10 () 12)))  {1,3,4,5,10,12}
{1,3,4,5,10,12}
(dica: use suas funções para manipulação de árvores binárias
(vazia?, raiz, etc).
Se você percorrer a árvore da maneira adequada,
os elementos aparecerão naturalmente em ordem crescente.
A maior dificuldade deste exercício é colocar as vírgulas de
maneira correta.)
Exercício 4.4: Uma maneira de mostrarmos uma árvore binária é colocando um
valor em cada linha;
primeiro a raiz, em seguida a sub-árvore esquerda e depois
a sub-árvore direita.
De modo a facilitar a identificação de cada sub-árvore,
identamos cada nova sub-árvore com 4 espaços em branco
a mais que sua raiz.
Uma árvore vazia pode ser mostrada como um simples traço (-),
e folhas não precisam mostrar suas sub-árvores.
Assim, por exemplo, a árvore da figura 3.2
seria exibida como:
A
B
-
E
H
C
F
G
I
J
Escreva um procedimento que, dada uma lista representando
uma árvore binária, exiba a árvore da forma descrita acima.
(dica: use a função mostra-n, do exemplo 4.2,
para fazer a identação.)
Exemplo 4.4:
Um uso bastante frequente de display é para acompanharmos
a execução de um determinado programa.
De maneira geral, qualquer função na forma
(define f
(lambda (a b)
...))
pode ser reescrita como
(define f
(lambda (a b)
(begin (display a) (newline) (display b) (newline)
...)))
Com isso, cada vez que a função é chamada,
ela mostra no terminal seus parâmetros.
Assim, temos uma maneira de saber quando a função está sendo chamada,
com que valores, etc.
Isso é útil tanto para entendermos melhor o funcionamento
de uma dada função quanto para detectarmos erros em alguma
função que não esteja funcionando corretamente.
A função read permite lermos dados do terminal durante
a execução de um programa.
Quando chamada,
essa função espera até que o usuário entre com um valor no teclado;
esse valor é então retornado pela função read.
Exemplo 4.5: Uma chamada como
(+ (read) (read))
irá esperar o usuário (você!) entrar com dois números,
e em seguidá imprimirá sua soma.16
Usualmente,
um read é precedido por um display com uma
mensagem avisando ao usuário que ele deve entrar com algum
dado (um prompt, em inglês).
Assim, o exemplo acima poderia ser reescrito como:
(begin (display "Entre com dois números")
(newline)
(+ (read) (read)))
Exercício 4.5: Defina funções para as tarefas abaixo:
-
Pedir um número ao usuário,
e em seguida mostrar a mensagem
"O seno de x é sin x",
onde x é o valor fornecido e sin x o seu seno.
(dica: use let para guardar o valor lido.)
-
Repetidamente pedir um número ao usuário,
até este entrar com o número 0,
e retornar a soma dos números lidos.
 Repetidamente pedir um número ao usuário,
até este entrar com o número 0,
e retornar uma lista com todos os números lidos,
na mesma ordem em que eles foram dados.
Repetidamente pedir um número ao usuário,
até este entrar com o número 0,
e retornar uma lista com todos os números lidos,
na mesma ordem em que eles foram dados.
-
Pedir um número n ao usuário,
em seguida ler mais n números,
e retornar uma lista com esses n números.
-
Repetidamente pedir um número ao usuário,
até este entrar com o número 0,
e mostrar a soma e o produto dos números lidos
(não incluir o 0).
4.2 : Vetores
Vetores (ou arrays, como são chamados em outras linguagens)
são estruturas de dados de certo modo similares a listas,
no sentido que também armazenam uma sequência de valores.
Entretanto, enquanto em listas só podemos manipular diretamente
o primeiro elemento, através de car,
vetores permitem o que chamamos de acesso direto.
Isso significa que podemos consultar e/ou alterar diretamente
qualquer elemento de um vetor.
Vetores em Scheme são representados textualmente
entre um #( e um ).
Por exemplo, a expressão
#(3 19 (8 9) 4)
representa um vetor com 4 elementos.
Assim como listas,
para descrevermos diretamente um vetor em Scheme
devemos usar o quote.
Por exemplo, para definir v como sendo o vetor acima,
escrevemos
(define v '#(3 19 (8 9) 4))
Para acessarmos um elemento qualquer de um vetor,
usamos a função vector-ref.
Essa função recebe o vetor a ser consultado e um índice,
um número natural que indica a posição do elemento
que queremos consultar.
Em Scheme, a indexação de vetores começa sempre com 0;
assim, para acessarmos o primeiro elemento usamos o índice 0,
para o segundo elemento o índice 1, etc.
Em particular, em um vetor com n elementos,
o índice do último elemento será n-1.
Por exemplo, se v está definido como acima, teremos:
(vector-ref v 0)  3
3
(vector-ref v 1)  19
19
(vector-ref v 2)  (8 9)
(8 9)
(vector-ref v 3)  4
4
Se tentarmos executar (vector-ref v 4) teremos um erro,
pois não existe posição 4 no vetor v.
A função vector-length retorna o número de elementos
de um vetor.
Em particular, a expressão (- (vector-length v) 1)
retorna o índice do último elemento de um vetor.
Exercício 4.6:
- Defina uma variável contendo um vetor com os
elementos 1, 2, 4, 5, e 10.
- Defina uma função que receba um vetor e retorne seu último elemento.
 Defina uma função que receba um vetor de números e
retorne a média aritmética entre o primeiro e o último elementos.
Defina uma função que receba um vetor de números e
retorne a média aritmética entre o primeiro e o último elementos.
- Defina uma função que receba um vetor de números e
retorne a soma de seus três primeiros elementos.
- Defina uma função que receba um vetor e um índice i,
e retorne a média dos valores nas posições i e i+1.
- Defina um predicado que receba um vetor e dois índices
i e j, e verifique se os valores nas posições i e j
do vetor são iguais.
Como a única maneira de se acessar um elemento de um vetor
é através de um índice,
a recursão sobre vetores é bastante diferente da recursão sobre
listas.
Ao invés de usarmos car, cdr e null?,
devemos usar um índice variando de um em um,
passando assim por todos os elementos do vetor.
A função vector-length pode ser usada
para saber em que índice parar (ou começar) a recursão.
Exemplo 4.6: Para somarmos os elementos de um vetor,
podemos definir uma função como abaixo,
usando recursão final:
(define soma-aux
(lambda (v i s)
(if (= i (vector-length v))
s
(soma-aux v (+ i 1) (+ s (vector-ref v i))))))
(define soma (lambda (v) (soma-aux v 0 0)))
Na função soma-aux,
v é o vetor cujos elementos estamos somando,
i percorre os índices,
e s acumula o resultado.
O traço dessa função,
quando chamada sobre o vetor #(2 5 3),
será:
(soma '#(2 5 3))

(soma-aux '#(2 5 3) 0 0)

(soma-aux '#(2 5 3) 1 2)

(soma-aux '#(2 5 3) 2 7)

(soma-aux '#(2 5 3) 3 10)
 fim, pois
fim, pois i = (vector-length v)
10  resultado final
resultado final
Essa mesma função pode ser escrita,
de forma mais compacta, usando-se o do:
(define soma
(lambda (v)
(do ((i 0 (+ i 1))
(s 0 (+ s (vector-ref v i))))
((= i (vector-length v)) s))))
Exemplo 4.7: Como podemos acessar os elementos do vetor diretamente,
isto é, em qualquer ordem,
podemos reescrever a função soma somando os elementos
do último para o primeiro.
Como a terminação é quando i passar de 0,
só precisamos chamar vector-length uma única vez,
no início da repetição.
Nesse caso, a função pode ser escrita como:
(define soma
(lambda (v)
(do ((i (- (vector-length v) 1) (- i 1))
(s 0 (+ s (vector-ref v i))))
((< i 0) s))))
Note que i começa com o tamanho do vetor menos 1,
que é o último índice do vetor.
Exercício 4.7: Defina as seguintes funções:
- Uma função que retorne o produto dos elementos de um vetor.
 Uma função que retorne uma lista com os elementos de um vetor.17
Uma função que retorne uma lista com os elementos de um vetor.17
- Uma função
busca
que verifique se um dado elemento existe em
alguma posição do vetor.
Caso positivo, a função deve retornar o índice onde esse
elemento foi encontrado;
caso contrário, retorna ().
Por exemplo,
(busca '#(banana pera uva goiaba) 'uva)  2
2
(busca '#(banana pera uva goiaba) 'pitanga)  ()
()
- Uma função que imprima os elementos de um vetor,
um por linha.
- Uma função
maior que retorne o maior elemento
em um vetor de números.
Por exemplo,
(maior '#(10 8 5 19 3 -8))  19
19
Exercício 4.8:  Defina uma função
Defina uma função indice-maior
que retorne o índice do maior elemento em um vetor de números.
Essa função deve receber, além do vetor, um índice indicando
até que elemento procurar.
Por exemplo,
(indice-maior '#(10 8 5 19 3 -8) 5)  3
3
pois o maior valor do vetor, 19, está na posição 3;
enquanto
(indice-maior '#(10 8 5 19 3 -8) 2)  0
0
pois o maior elemento até o índice 2 (isto é, entre os 3 primeiros
elementos) é 10, na posição 0.
Exercício 4.9:
Considere um vetor onde cada elemento é uma lista com
um símbolo e um número, como por exemplo:
(define v #((u 1) (r 2) (s 5) (c 0) (c 7) (o -1) (i 4) (c -1)))
O número em cada posição do vetor é usado para
indicar uma próxima posição no vetor, formando um encadeamento.
Por exemplo, na posição 3 de v temos a lista (c 0),
indicando que a próxima posição no encadeamento é a posição 0.
Na posição 0 temos (u 1),
indicando o 1 como a próxima posição.
O valor -1 em uma posição indica o fim de uma cadeia.
Escreva uma função cadeia que,
dados um vetor como descrito acima,
e uma posição inicial,
retorne a lista com os símbolos contidos nas posições encadeadas.
Por exemplo, com v declarado como acima, teríamos:
(cadeia v 3)  (c u r s o)
(c u r s o)
(cadeia v 6)  (i c c)
(i c c)
O procedimento vector-set! permite
alterarmos o valor de qualquer posição de um vetor.
Esse procedimento recebe o vetor a ser alterado,
o índice,
e o novo valor a ser colocado naquele índice.
O valor antigo é simplesmente apagado.
Por exemplo, se definirmos
(define vet '#(2 90 -9 0.1))
e executarmos
(vector-set! vet 2 13)
após essa operação vet será '#(2 90 13 0.1).
Vale a pena frizar que, ao contrário de cons para listas,
vector-set! não cria um novo vetor,
mas modifica o valor armazenado em uma dada
posição de um vetor pré-existente.
Também é importante lembrar que vector-set! é um procedimento.
O valor retornado por essa função é irrelevante.
Usamos vector-set! somente para modificar um valor em uma
posição de um dado vetor.
Exemplo 4.8: Queremos um procedimento
zera-vetor que receba um vetor,
e coloque 0 em todas as suas posições.
A melhor maneira de definirmos essa função é com um do:
(define zera-vetor
(lambda (v)
(do ((i 0 (+ i 1)))
((= i (vector-length v)))
(vector-set! v i 0))))
Note que o vector-set! é usado no corpo do do,
pois ele só executado por seu efeito sobre o vetor.
Exercício 4.10: Escreva um procedimento que receba um vetor de números e seu tamanho,
e coloque em cada posição do vetor seu antigo valor mais 1.
Exercício 4.11:  Defina um procedimento
Defina um procedimento troca que receba um vetor e
dois índices, e troque os valores nas posições dos índices um pelo outro.
Exercício 4.12: O que faz o procedimento abaixo?
(define s-aux
(lambda (v i)
(if (> i 0)
(begin
(troca v i (indice-maior v i))
(s-aux v (- i 1))))))
(define s (lambda (v) (s-aux v (- (vector-length v) 1))))
Lembre-se que as funções troca e indice-maior foram
definidas nos exercícios 4.11 e 4.8,
respectivamente.
(dica: faça o traço da chamada (s '#(7 8 12 10 6)))
O uso de quote para criarmos vetores é bastante
adequado para nossos pequenos exemplos,
mas quando queremos construir vetores maiores
(por exemplo, com mil elementos),
ou dinamicamente dentro de uma função,
precisamos de uma função que crie novos vetores.
Ao contrário de listas,
que podem ser criadas elemento por elemento
com a função cons,
vetores são criados em uma única operação,
com um tamanho pré-determinado.
A função make-vector faz isso:
recebe como parâmetro um número n e retorna um
novo vetor com n posições.
Esse novo vetor tem todas as suas posicões inicializadas
com (), a lista vazia.
Por exemplo,
(make-vector 8)  #(() () () () () () () ())
#(() () () () () () () ())
Essa diferença na forma de criarmos vetores e listas
implica diferenças na forma de programarmos usando um ou outro.
Com listas, é comum termos funções que usam cons recursivamente,
contruindo uma lista elemento por elemento.
Com vetores, raramente usamos make-vector
dentro de uma função recursiva,
a não ser que nosso objetivo seja criar vários vetores.
Em geral, criamos o vetor e então chamamos uma função recursiva
para operar sobre seus elementos, um a um.
Exemplo 4.9: Considere uma função que receba um número n e
retorne um vetor de n elementos contendo 0 em todas
as suas posições.
Para isso, basta criarmos o vetor com make-vector,
chamarmos o procedimento zera-vetor,
definido no exemplo 4.8,
e em seguida retornar esse vetor:
(define cria-zeros
(lambda (n)
(let ((v (make-vector n)))
(begin
(zera-vetor v)
v))))
Exemplo 4.10: Considere uma função que receba uma lista e crie um
vetor contendo os mesmos elementos da lista.
Podemos definir essa função como se segue:18
(define lista->vetor-aux
(lambda (v i l)
(if (null? l)
v
(begin
(vector-set! v i (car l))
(lista->vetor-aux v (+ i 1) (cdr l))))))
(define lista->vetor (lambda (l)
(lista->vetor-aux (make-vector (length l)) 0 l)))
A função lista->vetor calcula o tamanho da lista l,
usando a função length, e cria um vetor do mesmo tamanho.
Em seguida, chama a função auxiliar lista->vetor-aux
para preencher o vetor com os valores da lista.
Nesse exemplo, como o vetor foi explicitamente criado com o
mesmo tamanho da lista,
a recursão e o vetor terminam quando a lista terminar.
Exercício 4.13: Escreva o traço da chamada (lista->vetor '(a b c d)).
Exercício 4.14: Reescreva a função lista->vetor usando do.
Exercício 4.15: Escreva uma função soma-vetor,
que receba dois vetores de números com o mesmo tamanho,
e retorne um novo vetor com a soma dos elementos dos vetores
dois a dois.
Por exemplo:
(soma-vetor '#(1 3 5) '#(8 7 8))  #(9 10 13)
#(9 10 13)
Exercício 4.16:  Escreva uma função
Escreva uma função cria-vetor
que receba um tamanho n e uma função f,
e retorne o vetor composto pelos valores
f(0), f(1), ..., f(n-1).
Por exemplo,
(cria-vetor 5 (lambda (x) (* x 2)))  #(0 2 4 6 8)
#(0 2 4 6 8)
(cria-vetor 4 (lambda (x) 1))  #(1 1 1 1)
#(1 1 1 1)
Exercício 4.17: Refaça o exercício 4.15 usando
a função cria-vetor.
Exercício 4.18:
Um uso bastante comum de vetores é para a
representação de matrizes.
Uma matriz pode ser representada por um vetor de linhas,
onde cada linha é um vetor de colunas.
Por exemplo,
podemos representar a matriz
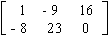 através do vetor
através do vetor
#(#( 1 -9 16) #(-8 23 0))
 Escreva uma função que receba dois parâmetros m e n
e retorne uma matriz de zeros de tamanho m × n.
Por exemplo
Escreva uma função que receba dois parâmetros m e n
e retorne uma matriz de zeros de tamanho m × n.
Por exemplo
(make-matrix 3 2)  #(#(0 0) #(0 0) #(0 0))
#(#(0 0) #(0 0) #(0 0))
(dica: use a função cria-vetor.)
- Escreva uma função
matrix-ref que receba uma matriz a
e dois índices i e j,
e retorne o valor do elemento ai j.
- Escreva uma função
matrix-set! que receba uma matriz a,
dois índices i e j, e um valor v,
e modifique o valor da posição ai j para v.
 Escreva uma função
Escreva uma função cria-matriz,
que receba m, n, e uma função f,
e retorne uma nova matriz de tamanho m × n,
onde cada elemento ai j tem o valor de f(i,j).
Por exemplo,
(cria-matriz 3 3 +)  #(#(0 1 2) #(1 2 3) #(2 3 4))
#(#(0 1 2) #(1 2 3) #(2 3 4))
(dica: use a função cria-vetor.)
- Escreva uma função que receba duas matrizes e seus tamanhos,
e retorne a matriz com o produto das duas matrizes dadas.
Para lembrar, o produto de uma matriz a de tamanho n × m por uma
matriz b de m × k, é uma matriz c de tamanho n × k,
com seus elementos definidos pela fórmula
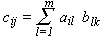 (dica: procure escrever uma função para calcular
o somatório acima,
e use a função
(dica: procure escrever uma função para calcular
o somatório acima,
e use a função cria-matriz para construir o resultado.)
Listas × Vetores
Listas e vetores são, até certo ponto,
intercambiáveis.
Qualquer estrutura que pode ser representada
com listas pode ser representada com vetores,
e vice-versa.
Entretanto, as dificuldades e o desempenho associados
a cada representação podem ser bem diferentes.
De maneira geral, listas são mais flexíveis e mais simples de usar,
pois não precisam ser previamente criadas com um tamanho fixo;
ao contrário, listas vão sendo construídas a medida que seus valores
vão aparecendo.
Por outro lado, a memória de computadores tem um funcionamento
bastante similar a um enorme vetor.
Por isso, vetores têm, em qualquer linguagem,
implementações bem mais eficientes do que listas.
Por exemplo, o acesso ao milésimo elemento de um vetor é uma
operação bastante simples para o computador.
Já acessar o milésimo termo de uma lista exige percorrer todos
os 999 elementos anteriores.
Além disso, representação de matrizes usando vetores
é bem mais direta que com listas;
portanto, muitos programas de manipulação numérica,
que fazem intenso uso de matrizes,
usam exclusivamente vetores.
A maioria dos programas reais usam representações de dados
(ou estruturas de dados) mais complexas que listas
ou vetores simples, muitas vezes envolvendo uma
combinação de ambos.
Capítulo 5 :
Solução de Alguns Exercícios Selecionados
Exercício 1.1.k: (+ 1 2 3 4 5 6 7 8 9).
Tanto o operador + quanto
o operador * podem receber mais de dois argumentos.
Exercício 1.1.q: (+ (sin 4.5) (cos 3.7))
Exercício 1.2.d: 3.1 × (2 + 5.4)
Exercício 1.2.q: sin x + cos x
Exercício 1.2.r: sin (x + cos x)
Exercício 1.3.f: (- (/ 5 2) (quotient 5 2))
Exercício 1.3.g: (+ (* (quotient 1345 17) 17) (remainder 1345 17))
Exercício 1.7.e: O símbolo a será associado ao operador de soma.
Após essa definição, você pode escrever (a 4 5) para somar
4 e 5.
Exercício 1.13.a: caar, pois o valor de (caar l) é:
(caar l)
 definição de
definição de caar
(car (car l))
 valor de
valor de l
(car (car '((a b c) (e f) g)))

(car '(a b c))

'a 
Exercício 1.13.e: cadadr. Fazendo o traço:
(cadadr l)
 definição de
definição de cadadr
(car (cdr (car (cdr l))))
 valor de
valor de l
(car (cdr (car (cdr '((a b c) (e f) g)))))

(car (cdr (car '((e f) g))))

(car (cdr '(e f)))

(car '(f))

'f

Exercício 1.14.a: (define dobro (lambda (x) (* x 2)))
ou então (define dobro (lambda (x) (+ x x))).
Exercício 1.14.g: (define f (lambda (x y) 10))
Exercício 1.14.k: (define f (lambda (x y z) (- (+ (* 10 x) (* 5 y)) z)))
Exercício 1.14.n: (define segundo (lambda (l) (cadr l)))
Ou mais diretamente:
(define segundo cadr)
Exercício 1.16.d:
(((lambda (x) (lambda (y) (- x y))) 4) 5)
 1o lambda,
com {
1o lambda,
com {x 4}
4}
((lambda (y) (- 4 y)) 5)
 lambda, com {
lambda, com {y 5}
5}
(- 4 5)
 aritmética
aritmética
-1 
Exercício 1.18.b: (define maior5 (lambda (x) (> x 5)))
Exercício 1.18.e: Testar se 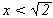 é o mesmo que testar
se x2 < 2; em Scheme:
é o mesmo que testar
se x2 < 2; em Scheme:
(define mr2 (lambda (x) (< (* x x) 2)))
Exercício 1.21.f:
Uma lista tem pelo menos dois elementos quando 1) ela não é vazia, e 2) não fica vazia se lhe tirarmos um elemento.
Em Scheme:
(define len2?
(lambda (l)
(and (not (null? l))
(not (null? (cdr l))))))
Usando cond, podemos reescrever len2? como:
(define len2?
(lambda (l)
(cond
((null? l) #f)
((null? (cdr l)) #f)
(else #t))))
Exercício 1.23.c: O predicado (and (> x 5) (<= x 10)) é verdadeiro quando x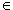 (5,10]. Portanto, o predicado
(5,10]. Portanto, o predicado (not (and (> x 5) (<= x 10))) é
verdadeiro quando x estiver fora desse intervalo.
Uma outra forma de dizer que x está fora de um intervalo
é dizer que, ou ele está abaixo do intervalo (x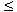 5),
ou que ele está acima (x>10).
Em Scheme,
5),
ou que ele está acima (x>10).
Em Scheme, (or (<= x 5) (> x 10)).
Exercício 2.2.d: Ao contrário de várias outras funções,
não faz muito sentido definirmos a função máximo para uma lista vazia
(mais formalmente, podemos dizer que a operação max
não tem elemento neutro).
Assim, nosso caso base será a lista com um único elemento,
onde o maior elemento da lista é esse único valor.
Para o caso recursivo, supomos que temos o resultado
da chamada recursiva, (maximo (cdr l)).
Tendo esse valor, qual o valor máximo da lista l?
Ou é esse valor, ou é (car l), dependendo qual deles é maior.
Mas para comparar apenas dois número já temos uma função pronta,
chamada max.
Juntando tudo, teremos:
(define maximo
(lambda (l)
(if (null? (cdr l)) ; ultimo/unico elemento?
(car l)
(max (car l) (maximo (cdr l))))))
Note que a função não está definida para a lista vazia.
Exercício 2.2.e:
(define pares?
(lambda (l)
(if (null? l)
#t
(and (even? (car l))
(pares? (cdr l))))))
Exercício 2.5.a:
(define n-esimo
(lambda (n l)
(if (= n 1) ; primeiro elemento?
(car l)
(n-esimo (- n 1) (cdr l)))))
Note que, se n for maior que o comprimento da lista,
a lista irá terminar antes de n chegar a 1,
e teremos um erro ao aplicar cdr sobre a lista vazia.
Exercício 2.6.i:
(define pos-aux
(lambda (e l n)
(cond
((null? l) '())
((equal? e (car l)) n)
(else (pos-aux e (cdr l) (+ n 1))))))
(define pos (lambda (e l) (pos-aux e l 1)))
Exercício 2.21.c:
(define comp (lambda (l) (acumula 0 (lambda (a e) (+ a 1)) l)))
Observação:
dependendo da maneira como você implementou a função acumula,
podem ser necessárias pequenas modificações na solução acima,
como por exemplo trocar a ordem dos parâmetros
a (acumulador) e e (elemento),
ou mesmo a ordem dos argumentos na chamada de acumula.
Exercício 2.25: Fazendo uma tradução mecânica, teríamos:
(define media-aux
(lambda (l l1 s n)
(if (null? l1)
(/ s n)
(media-aux l (cdr l1) (+ s (car l1)) (+ n 1)))))
(define media (lambda (l) (media-aux l l 0 0)))
Em uma implementação normal, não precisaríamos do parâmetro l
na função media-aux, pois ele não é utilizado.
Exercício 2.27.h:
Uma implementação normal para essa função,
usando-se recursão final,
é mostrada abaixo:
(define conta-aux
(lambda (l1 e n)
(if (null? l1)
n
(if (equal? e (car l1))
(conta-aux (cdr l1) e (+ n 1))
(conta-aux (cdr l1) e n)))))
(define conta (lambda (l e) (conta-aux l e 0)))
Mas não sabemos como passar dessa forma para o do,
pois temos duas ocorrências da chamada recursiva.
Entretanto, a função conta-aux pode ser reescrita como abaixo,
onde usamos o if diretamente no cálculo do novo valor de n:
(define conta-aux
(lambda (l1 e n)
(if (null? l1)
n
(conta-aux (cdr l1) e (if (equal? e (car l1)) (+ n 1) n)))))
Agora, podemos transformar a recursão final para do diretamente:
(define conta
(lambda (l e)
(do ((l1 l (cdr l1))
(n 0 (if (equal? e (car l1)) (+ n 1) n)))
((null? l1) n))))
Exercício 3.16.b:
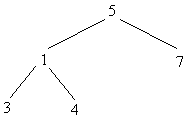 Exercício 3.17: Lembrando que as sub-árvores de uma
folha são árvores vazias, temos:
Exercício 3.17: Lembrando que as sub-árvores de uma
folha são árvores vazias, temos:
(define esquerda
(lambda (a)
(if (folha? a)
arvore-vazia
(cadr a))))
A função direita é definida analogamente.
Assim como raiz, essas funções não estão definidas
sobre a árvore vazia.
Exercício 3.20.d: Considerando que 3+4+5 é na
realidade (3+4)+5, teremos a árvore:
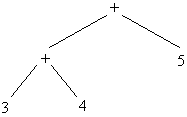 Na representação pré-fixada, essa árvore resulta na lista
Na representação pré-fixada, essa árvore resulta na lista
(+ (+ 3 4) 5);
na representação in-fixada, temos ((3 + 4) + 5);
e na pós-fixada, ((3 4 +) 5 +).
Exercício 3.25:
Se a árvore tem uma sub-árvore esquerda não vazia,
seu menor elemento está nessa sub-árvore.
Caso contrário, seu menor elemento é a própria raiz:
(define menor
(lambda (a)
(if (vazia? (esquerda a))
(raiz a)
(menor (esquerda a)))))
Note que essa função não funcionará corretamente se
chamada com a árvore vazia;
isso apenas reflete o fato de que o valor do menor
elemento de uma árvore vazia não é bem definido.
Exercício 3.27:
(define insere
(lambda (e a)
(cond
((vazia? a) (cria-arvore e arvore-vazia arvore-vazia))
((= e (raiz a)) a)
((< e (raiz a)) (cria-arvore (raiz a)
(insere e (esquerda a))
(direita a)))
(else (cria-arvore (raiz a)
(esquerda a)
(insere e (direita a)))))))
Exercício 4.1.d:
A dificuldade neste exercício é saber quando mudar de linha.
Uma solução convencional para esse problema é usarmos um contador,
que nos diz quantos elementos já foram impressos.
Sempre que esse contador for par, é hora de mudar de linha;
caso contrário, apenas damos um espaço:
(define (mostra-lista-aux l i)
(if (not (null? l))
(begin
(display (car l))
(if (even? i) (newline) (display " "))
(mostra-lista-aux (cdr l) (+ i 1)))))
(define (mostra-lista l) (mostra-lista-aux l 1))
O procedimento acima pode ser diretamente traduzido para usar um do:
(define (mostra-lista l)
(do ((l l (cdr l))
(i 1 (+ i 1)))
((null? l))
(display (car l))
(if (even? i) (newline) (display " "))))
Exercício 4.3.a:
Existem dois detalhes nesse procedimento.
Primeiro, como o par de chaves deve ser mostrado uma
única vez, em torno de uma repetição de elementos,
sua exibição deve ser feita fora da repetição.
Segundo, como as vírgulas aparecem entre os elementos,
para n elementos temos apenas n-1 vírgulas.
Uma solução para isso é só mostrarmos a vírgula após um
elemento se ele não for o último.
(define mostra-elementos
(lambda (l)
(do ((l l (cdr l)))
((null? l))
(display (car l))
(if (not (null? (cdr l))) (display ",")))))
(define mostra-conjunto
(lambda (c)
(begin
(display "{")
(mostra-elementos c)
(display "}")
(newline))))
Exercício 4.5.c:
(define le-lista
(lambda ()
(let ((v (read)))
(if (zero? v)
'(0)
(cons v (le-lista))))))
Exercício 4.6.c:
(define f
(lambda (v)
(/ (+ (vector-ref v 0)
(vector-ref v (- (vector-length v) 1)))
2)))
Exercício 4.7.b:
(define vetor-lista-aux
(lambda (v i)
(if (= i (vector-length v))
'()
(cons (vector-ref v i) (vetor-lista-aux v (+ i 1))))))
(define vetor-lista (lambda (v) (vetor-lista-aux v 0)))
Exercício 4.8:
(define indice-maior
(lambda (v i)
(if (= i 0)
0
(let ((m (indice-maior v (- i 1))))
(if (>= (vector-ref v i) (vector-ref v m))
i
m)))))
Exercício 4.11:
(define troca
(lambda (v i j)
(let ((vi (vector-ref v i))
(vj (vector-ref v j)))
(vector-set! v i vj)
(vector-set! v j vi))))
Exercício 4.16:
Para essa função, precisamos primeiro criar um vetor,
depois preenchê-lo com os valores f(0), f(1), ..., f(n-1),
e finalmente retornar o próprio vetor.
(define cria-vetor
(lambda (n f)
(do ((v (make-vector n) v)
(i 0 (+ i 1)))
((= i n) v)
(vector-set! v i (f i)))))
Observe o v como valor final do do,
que por sua vez é o valor final da função.
Exercício 4.18.a:
A função
(lambda (i) (cria-vetor n (lambda (j) 0)))
é uma função que, quando chamada com qualquer argumento,
cria um vetor com n zeros.
Portanto, colocando essa função como argumento de outro
cria-vetor, temos uma expressão que cria um vetor
onde cada elemento é um vetor com n zeros,
ou seja, uma matriz de zeros:
(define cria-matriz-zeros
(lambda (n m)
(cria-vetor n (lambda (i)
(cria-vetor m (lambda (j) 0))))))
Notas de Pé de Pagina
(1)
Nesse tipo de exercício,
primeiro tente calcular o valor da expressão sem o uso do computador.
Sempre que possível, faça o traço da avaliação.
Procure usar o computador apenas para verificar sua resposta.
(2)
Na realidade, podemos aplicar cons sobre quaisquer valores.
O resultado, em geral, não será uma lista, mas um par,
que é escrito como (a . b).
Esse tipo de estrutura, entretanto, foge do escopo deste texto.
(3)
Lambda é o nome da letra grega 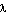 .
Essa notação para funções é baseada no
.
Essa notação para funções é baseada no
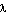 -cálculo, uma teoria criada na década de 40
pelo matemático A. Church.
Em uma notação mais `matemática',
a definição de
-cálculo, uma teoria criada na década de 40
pelo matemático A. Church.
Em uma notação mais `matemática',
a definição de f poderia ser escrita como
f = 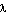 x . 2x.
(4)
Em várias implementações de Scheme,
a lista vazia
x . 2x.
(4)
Em várias implementações de Scheme,
a lista vazia () pode ser usada no lugar de #f,
para representar o valor falso.
(5)
Essa função é pré-definida em Scheme sob o nome length.
(6)
Essa função é pré-definida em Scheme sob o nome member.
(7)
Essa função é pré-definida em Scheme sob o nome append.
(8)
Essa função é pré-definida em Scheme sob o nome reverse.
(9)
Essa formulação do princípio de indução é um
pouco diferente da formulação tradicional.
A nosso ver, ela é melhor adaptada para problemas ligados
a funções recursivas.
Para quem já conhece o princípio de indução,
a formulação colocada aqui pode ser justificada associando-se,
a cada chamada da função, um natural n igual ao
número de chamadas recursivas que a função faz até terminar.
Cada chamada recursiva tem um n menor que a chamada original,
pois exigimos que a função termine;
o caso base, n=0,
corresponde às situações em que a função não faz chamadas recursivas.
Logo, pelo princípio de indução forte,
podemos usar a correção dessas chamadas nas nossas hipóteses.
(10)
Para alguns tipos de função,
como a função de Ackerman,
esse método para provar terminação não é suficiente.
Mas tais casos são algo exóticos,
e fogem do escopo deste texto.
(11)
Essa função é pré-definida em Scheme sob o nome map.
(12)
Como Scheme já tem uma função pré-definida
chamada zero?, para evitar confusão
vamos usar o nome zer? para nosso predicado.
(13)
O leitor mais atento perceberá que existe um
pequeno `roubo' nessa definição:
se não temos números, não podemos executar a operação (+ (car n) 1)
indicada.
Como (car n) é necessariamente um único dígito,
esse incremento poderia ser definido por casos.
Mas, para evitar mais complexidade, vamos assumir que essa soma
restrita a dígitos simples é válida
(14)
Várias linguagens, notadamente Pascal,
tem explícito o conceito de procedimentos.
Nessas linguagens, um procedimento não retorna nenhum valor.
Scheme não oferece tal conceito,
portanto procedimentos têm que ser implementados
através de funções.
Por isso, nossos `procedimentos' sempre retornam algum valor,
mas vamos sempre ignorar esse valor.
(15)
Em Scheme, muitas construções tem o chamado
begin implícito, entre elas
lambda, let e if.
Isso significa que podemos usar várias expressões em
sequência no corpo dessas construções sem necessidade
de um begin.
Entretanto, por razões didáticas, vamos
sempre usar o begin explicitamente.
(16)
No princípio dos tempos,
computadores não tinham terminais com telas,
e toda saída de dados era impressa em papel, cartão, ou algum outro meio.
Como programadores são bastante conservadores,
o termo imprimir ainda é usado no jargão da área
como sinônimo de exibir algo no terminal.
(17)
Essa função é pré-definida em Scheme sob o
nome vector->list.
(18)
Essa função é pré-definida em Scheme sob o
nome list->vector.
 1+2+3+4+5+6+7+8+9
1+2+3+4+5+6+7+8+9
 sin 4.5 + cos 3.7
sin 4.5 + cos 3.7
 1+2+3+4+5+6+7+8+9
1+2+3+4+5+6+7+8+9
 sin 4.5 + cos 3.7
sin 4.5 + cos 3.7



 ( a b ( c) )
( a b ( c) )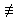 (ab (c))
(ab (c)) executa multiplicação
executa multiplicação executa multiplicação
executa multiplicação executa soma
executa soma resultado final
resultado final (+ -40 7.3 (* 2 7.3))
(+ -40 7.3 (* 2 7.3)) (+ (* 8 -5) 7.3 14.6)
(+ (* 8 -5) 7.3 14.6) valor de
valor de  valor de
valor de  valor de
valor de  executa multiplicação
executa multiplicação executa multiplicação
executa multiplicação executa soma
executa soma resultado final
resultado final v1,n2
v1,n2  v2,..., nn
v2,..., nn  vn}
vn} 28,
28,  89}.
Exercício 1.7: Qual o efeito das declarações abaixo, executadas em ordem?
89}.
Exercício 1.7: Qual o efeito das declarações abaixo, executadas em ordem?
 soma e seno
soma e seno corpo do
corpo do  17,
17, -0.544021}
-0.544021} ambiente local
ambiente local aritmética
aritmética resultado final
resultado final 17,
17, -0.544021}
-0.544021} 17,
17, -0.544021}.
-0.544021}.
 seno
seno corpo
do 1o
corpo
do 1o  -0.544}
-0.544} valor
de
valor
de  aritmética
aritmética corpo do
corpo do  -5.14425}
-5.14425} valor de
valor de  aritmética
aritmética
 5,
5,  10}.
Em seguida, calcule o valor das expressões abaixo:
10}.
Em seguida, calcule o valor das expressões abaixo: (3 4 5)
(3 4 5) ((4 5) 2)
((4 5) 2) a
a b
b x
x (cadr l)
(cadr l) (caar l)
(caar l) (cdar l)
(cdar l) (caaar l)
(caaar l) dobro(x) = 2x
dobro(x) = 2x
 f(x,y) = 10 (função constante com dois parâmetros)
f(x,y) = 10 (função constante com dois parâmetros)
 f(x,y,z) = 10x + 5y - z
f(x,y,z) = 10x + 5y - z
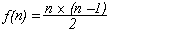
 uma função que retorne o segundo elemento de uma dada lista;
uma função que retorne o segundo elemento de uma dada lista;
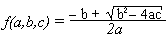
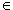
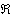 .
Já a pré-condição da função dada no exercício 1.14.n é
que seu argumento seja uma lista com comprimento maior ou igual a 2;
de outra forma, não podemos retornar seu segundo elemento.
Muitas vezes, não explicitamos as pré-condições de uma função.
No entanto, é muito importante que sempre tenhamos conciência do
domínio de validade de qualquer função que usamos.
Muitos erros em programas são causados por funções sendo chamadas
com argumentos inválidos ou não previstos.
Exercício 1.15: Descreva as pré-condições de cada uma das funções definidas
no exercício anterior.
Descreva também os domínios e contra-domínios dessas funções.
Conforme explicado acima,
o
.
Já a pré-condição da função dada no exercício 1.14.n é
que seu argumento seja uma lista com comprimento maior ou igual a 2;
de outra forma, não podemos retornar seu segundo elemento.
Muitas vezes, não explicitamos as pré-condições de uma função.
No entanto, é muito importante que sempre tenhamos conciência do
domínio de validade de qualquer função que usamos.
Muitos erros em programas são causados por funções sendo chamadas
com argumentos inválidos ou não previstos.
Exercício 1.15: Descreva as pré-condições de cada uma das funções definidas
no exercício anterior.
Descreva também os domínios e contra-domínios dessas funções.
Conforme explicado acima,
o  multiplicação
multiplicação valor de
valor de 
 72,
72,  3}.
Aplicando a regra toda, temos:
3}.
Aplicando a regra toda, temos:
 corpo do lambda
corpo do lambda 72,
72,  3}
3} valores
de
valores
de  aritmética
aritmética resultado final
resultado final ((lambda (n1 ... nn) corpo) e1 ... en)
((lambda (n1 ... nn) corpo) e1 ... en)

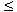 y e x
y e x  y, e pertinência em conjuntos (x
y, e pertinência em conjuntos (x 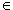 Y).
Chamamos esse tipo de função de predicado.
Predicados em Scheme são escritos como qualquer outra função,
mas retornam valores especiais que representam
verdadeiro ou falso.
Em Scheme, o valor verdadeiro é denotado pelo símbolo
Y).
Chamamos esse tipo de função de predicado.
Predicados em Scheme são escritos como qualquer outra função,
mas retornam valores especiais que representam
verdadeiro ou falso.
Em Scheme, o valor verdadeiro é denotado pelo símbolo 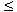 ,
este é escrito como
,
este é escrito como 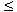 y vira
y vira  é escrito como
é escrito como  um predicado para verificar se um número é maior que 5;
um predicado para verificar se um número é maior que 5;
 um predicado para verificar se um número é
menor que
um predicado para verificar se um número é
menor que 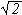 .
.
 0, e -x caso contrário.
Traduzindo a expressão acima para Scheme, teremos:
0, e -x caso contrário.
Traduzindo a expressão acima para Scheme, teremos:
 b
b c
c definição de
definição de  lambda, com
{
lambda, com
{ 3}
3} comparação
comparação regra do
regra do  comparação
comparação regra do
regra do 
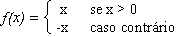
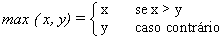
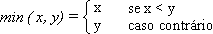
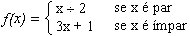
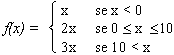
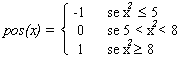 (dica: use
(dica: use  e
e (cond (c e') ...)
(cond (c e') ...) e
e (cond (a b) (else c))
(cond (a b) (else c)) (if c1 v1 (if c2 v2 v))
(if c1 v1 (if c2 v2 v)) c
c (cond (else c))
(cond (else c))  c
c b
b b
b #f
#f a
a a
a #t
#t (if a b #f)
(if a b #f) (if a #t b)
(if a #t b) (if a #f #t)
(if a #f #t) (if a c b)
(if a c b) lista tem pelo menos dois elementos;
lista tem pelo menos dois elementos;
 Reescreva os predicados abaixo,
sem usar o operador
Reescreva os predicados abaixo,
sem usar o operador 

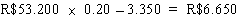 .
.
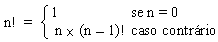
 corpo de fat
corpo de fat condicional
condicional corpo de
corpo de  condicional
condicional corpo de
corpo de  condicional
condicional corpo de
corpo de  condicional
condicional corpo de
corpo de  caso base
caso base multiplicação
multiplicação multiplicação
multiplicação multiplicação
multiplicação multiplicação
multiplicação resultado final
resultado final











 (1 1 1 1)
(1 1 1 1) ()
()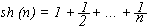
 uma função
uma função  um predicado para verificar se todos os números
de uma dada lista são pares;
um predicado para verificar se todos os números
de uma dada lista são pares;
 (2 5 7 3)
(2 5 7 3) (4 2 10 4)
(4 2 10 4) (a b c d e)
(a b c d e) (um gato maior que outro gato)
(um gato maior que outro gato) (2 3 4 5 8 9 10)
(2 3 4 5 8 9 10) (e d c b a)
(e d c b a) uma função que retorne o n-ésimo elemento de uma dada
lista, onde n é um parâmetro da função;
por exemplo:
uma função que retorne o n-ésimo elemento de uma dada
lista, onde n é um parâmetro da função;
por exemplo:
 c
c (a b novo d e f)
(a b novo d e f) (a b c d e)
(a b c d e) (3 4 10)
(3 4 10) #t
#t #f
#f definição + if
definição + if definição + if
definição + if definição + if
definição + if caso base
caso base
 definição de soma + if
definição de soma + if definição de soma + if
definição de soma + if definição de soma + if
definição de soma + if caso base
caso base valor do acumulador
valor do acumulador (5 4 3)
(5 4 3)



 caso base
caso base resultado final
resultado final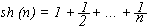
 uma função
uma função  2
2 ()
() (1 2 3 4 5)
(1 2 3 4 5) Escreva uma função para calcular
Escreva uma função para calcular
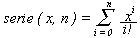
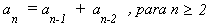
 (+ 8 -0.958924)
(+ 8 -0.958924) definição concreta de
definição concreta de  definição abstrata de
definição abstrata de  aritmética
aritmética resultado final (igual a 6!)
resultado final (igual a 6!) 0 temos que
0 temos que
 n!
n! definição concreta de
definição concreta de  seleção
seleção resultado final
resultado final 0!
0! definição concreta de
definição concreta de 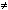 0)
0) definição abstrata de
definição abstrata de  (n-1)!
(n-1)! aritmética
aritmética resultado final
resultado final n × (n-1)! =
n × ((n-1) × ... × 1) = n!
n × (n-1)! =
n × ((n-1) × ... × 1) = n! n!
n! 0.
Esse raciocínio está correto, ou estamos blefando?
Afinal, estamos usando o fato que
0.
Esse raciocínio está correto, ou estamos blefando?
Afinal, estamos usando o fato que
 (n-1)!
para chegarmos a
(n-1)!
para chegarmos a  n!.
Não estamos andando em círculos?
A justificativa para o raciocínio que utilizamos é chamada
de princípio de indução.
Segundo o princípio de indução,
quando estamos verificando se uma função está corretamente definida,
podemos assumir que qualquer chamada recursiva da função
retornará a resposta correta,
desde que a função seja chamada com valores adequados
à sua pré-condição e
que a função termine.9
Antes de continuarmos,
é importante frizar que esse problema não é apenas teórico:
a função fatorial é muito simples, quase trivial,
mas para funções mais complexas pode ser bastante complicado
nos certificarmos que escrevemos a função corretamente.
Além disso, um programador experiente não pensa `concretamente'
sobre programas, mas abstratamente, ou indutivamente.
Ilustrativamente, podemos dizer que o programador iniciante,
é o que vê 120! como
120 × 119 × 118 × 117 × ...
× 5 × 4 × 3 × 2 × 1,
enquanto um programador experiente vê 120! como 120 × 119!.
n!.
Não estamos andando em círculos?
A justificativa para o raciocínio que utilizamos é chamada
de princípio de indução.
Segundo o princípio de indução,
quando estamos verificando se uma função está corretamente definida,
podemos assumir que qualquer chamada recursiva da função
retornará a resposta correta,
desde que a função seja chamada com valores adequados
à sua pré-condição e
que a função termine.9
Antes de continuarmos,
é importante frizar que esse problema não é apenas teórico:
a função fatorial é muito simples, quase trivial,
mas para funções mais complexas pode ser bastante complicado
nos certificarmos que escrevemos a função corretamente.
Além disso, um programador experiente não pensa `concretamente'
sobre programas, mas abstratamente, ou indutivamente.
Ilustrativamente, podemos dizer que o programador iniciante,
é o que vê 120! como
120 × 119 × 118 × 117 × ...
× 5 × 4 × 3 × 2 × 1,
enquanto um programador experiente vê 120! como 120 × 119!.
 a × xn
a × xn a = a × x0
a = a × x0 (exp x (n-1) (x × a))
(exp x (n-1) (x × a)) (x × a) × xn-1=a × xn
(x × a) × xn-1=a × xn 1 × xn = xn
1 × xn = xn 1=20
1=20 (/ (f (n+1)) 2)
(/ (f (n+1)) 2) 2n+1/2 = 2n
2n+1/2 = 2n




 0,
a condição 1 é satisfeita;
além disso, como a chamada recursiva é sobre n-1,
a condição 2 também é satisfeita.
Para muitas funções sobre listas,
podemos definir h como o comprimento da lista.
O comprimento é sempre um inteiro positivo (condição 1),
e
0,
a condição 1 é satisfeita;
além disso, como a chamada recursiva é sobre n-1,
a condição 2 também é satisfeita.
Para muitas funções sobre listas,
podemos definir h como o comprimento da lista.
O comprimento é sempre um inteiro positivo (condição 1),
e  b,
e mdc(a,b)=mdc(a,b-a), se b
b,
e mdc(a,b)=mdc(a,b-a), se b a.
Sua implementação em Scheme pode ser escrita como:
a.
Sua implementação em Scheme pode ser escrita como:
 b=mdc(0,b).
b=mdc(0,b).
 b --- Nesse caso,
b --- Nesse caso,
 (mdc (a-b) b)
(mdc (a-b) b) b, temos que a-b
b, temos que a-b  0,
garantindo a pré-condição na chamada recursiva.
Pelo princípio de indução,
0,
garantindo a pré-condição na chamada recursiva.
Pelo princípio de indução,
 mdc(a-b,b)
mdc(a-b,b) mdc(a,b)
mdc(a,b) 0.
Como a chamada recursiva só é feita se a e b forem
maiores que 0,
temos que a subtração necessariamente diminui seus valores. Portanto, 2) a cada nova chamada a soma a+b será menor que na
chamada anterior.
Logo, como vimos acima, a função termina.
0.
Como a chamada recursiva só é feita se a e b forem
maiores que 0,
temos que a subtração necessariamente diminui seus valores. Portanto, 2) a cada nova chamada a soma a+b será menor que na
chamada anterior.
Logo, como vimos acima, a função termina.
 b.
b. 0,
e que
0,
e que
 a × b
a × b Escreva uma função que retorne a lista dos fatores
primos de um dado número.
Por exemplo,
Escreva uma função que retorne a lista dos fatores
primos de um dado número.
Por exemplo,
 (2 2 3 7)
(2 2 3 7) 0, e que o produto dos elementos
da lista retornada é igual a n.
0, e que o produto dos elementos
da lista retornada é igual a n.
 (10 22 0)
(10 22 0) (1 5 3)
(1 5 3) (9 81 4)
(9 81 4)
 calcular o comprimento de uma lista;
calcular o comprimento de uma lista;
 contar quantas vezes um dado número aparece em uma lista;
contar quantas vezes um dado número aparece em uma lista;
 Usando a função
Usando a função  #f
#f #t
#t Identifique alguma função recursiva já
implementada por você que não possa ser reescrita sem o uso de recursão,
usando-se
Identifique alguma função recursiva já
implementada por você que não possa ser reescrita sem o uso de recursão,
usando-se 





 valor de s
valor de s Reescreva a função
Reescreva a função 

 (cdr l1)
(cdr l1) (+ s (car l1))
(+ s (car l1)) (+ n 1)
(+ n 1)
 (cdr l1)
(cdr l1) (+ s (car l1))
(+ s (car l1)) (+ n 1)
(+ n 1)
 (cdr l1)
(cdr l1) (+ s (car l1))
(+ s (car l1)) (+ n 1)
(+ n 1) predicado
predicado 
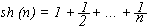
 uma função
uma função 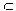 c2.
Exercício 3.5: Escreva um predicado que receba dois conjuntos c1 e c2 e verifique
se c1 = c2.
Observe que não basta comparar as listas.
Por exemplo, os conjuntos representados pelas listas
c2.
Exercício 3.5: Escreva um predicado que receba dois conjuntos c1 e c2 e verifique
se c1 = c2.
Observe que não basta comparar as listas.
Por exemplo, os conjuntos representados pelas listas
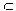 c2 e c2
c2 e c2 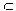 c1.)
Exercício 3.6: Redefina as funções de união e interseção de conjuntos
usando
c1.)
Exercício 3.6: Redefina as funções de união e interseção de conjuntos
usando  Reescreva as funções de união e interseção de conjuntos utilizando
a função
Reescreva as funções de união e interseção de conjuntos utilizando
a função  (1 1)
(1 1) (1 1 1 1 1 1)
(1 1 1 1 1 1) (1 1)
(1 1) (1)
(1) 2221111
2221111 (M-9611110 M-9523456)
(M-9611110 M-9523456) ("Paulo Moura" "Marta Silva Teles")
("Paulo Moura" "Marta Silva Teles")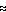 20).
Exercício 3.15: Considere um catálogo de telefones na sua casa:
20).
Exercício 3.15: Considere um catálogo de telefones na sua casa:
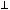 para representar as árvores vazias.
para representar as árvores vazias.

 Defina as funções
Defina as funções 
 3+4+5
3+4+5
 ((5 + 4) * (2 - 3))
((5 + 4) * (2 - 3))
 Defina uma função que retorne o menor elemento de
uma árvore de busca.
(dica: o menor elemento de uma árvore de busca está sempre no
seu `canto' mais esquerdo.)
Exercício 3.26: Escreva o predicado
Defina uma função que retorne o menor elemento de
uma árvore de busca.
(dica: o menor elemento de uma árvore de busca está sempre no
seu `canto' mais esquerdo.)
Exercício 3.26: Escreva o predicado  Escreva um predicado para inserir um novo elemento em uma
dada árvore de busca.
Se a árvore for vazia, retorne uma folha com o novo elemento.
Se o elemento a ser inserido for igual à raiz,
então ele já pertence a árvore,
e podemos retornar a árvore sem modificações.
Se ele for menor que a raiz, devemos inserí-lo na sub-árvore esquerda;
se for maior, na sub-árvore direita.
Antes de continuarmos, é importante frizar o que vimos nesta seção:
como diferentes representações para um mesmo tipo,
como listas × árvores de busca para conjuntos,
podem implicar em operações com desempenhos bastante desiguais.
Não por acaso, em geral representações com operações mais eficientes
envolvem implementações mais complexas.
O estudo de representações eficientes para diferentes tipos
de informação é uma das áreas centrais em computação.
Na próxima seção,
vamos ver uma outra representação para números naturais,
bem mais eficiente que a que vimos na seção 3.2.
Escreva um predicado para inserir um novo elemento em uma
dada árvore de busca.
Se a árvore for vazia, retorne uma folha com o novo elemento.
Se o elemento a ser inserido for igual à raiz,
então ele já pertence a árvore,
e podemos retornar a árvore sem modificações.
Se ele for menor que a raiz, devemos inserí-lo na sub-árvore esquerda;
se for maior, na sub-árvore direita.
Antes de continuarmos, é importante frizar o que vimos nesta seção:
como diferentes representações para um mesmo tipo,
como listas × árvores de busca para conjuntos,
podem implicar em operações com desempenhos bastante desiguais.
Não por acaso, em geral representações com operações mais eficientes
envolvem implementações mais complexas.
O estudo de representações eficientes para diferentes tipos
de informação é uma das áreas centrais em computação.
Na próxima seção,
vamos ver uma outra representação para números naturais,
bem mais eficiente que a que vimos na seção 3.2.

















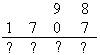 Para executarmos essa soma,
primeiro somamos os dois primeiros algarismos;
caso essa soma seja maior que 10 (a base),
diminuimos 10 do total e marcamos um `vai um'.
Para executarmos essa soma,
primeiro somamos os dois primeiros algarismos;
caso essa soma seja maior que 10 (a base),
diminuimos 10 do total e marcamos um `vai um'.
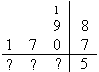 A seguir, repetimos exatamente os mesmos passos
para o resto dos dois números
(lidos da direita para a esquerda).
Isso é, somamos os dois primeiros algarismos e o `vai um',
verificamos se o resultado é maior que a base, etc.
Esse processo deve ser repetido até os dois números terminarem.
Porém, ocorre frequentemente de um dos números terminar antes
do outro.
No nosso exemplo, vamos chegar na seguinte situação:
A seguir, repetimos exatamente os mesmos passos
para o resto dos dois números
(lidos da direita para a esquerda).
Isso é, somamos os dois primeiros algarismos e o `vai um',
verificamos se o resultado é maior que a base, etc.
Esse processo deve ser repetido até os dois números terminarem.
Porém, ocorre frequentemente de um dos números terminar antes
do outro.
No nosso exemplo, vamos chegar na seguinte situação:
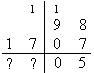 Nesse caso, simplesmente estendemos o número menor com um 0
e continuamos o processo:
Nesse caso, simplesmente estendemos o número menor com um 0
e continuamos o processo:
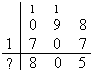 Quando finalmente os dois números terminarem,
chegamos ao fim da nossa operação:
Quando finalmente os dois números terminarem,
chegamos ao fim da nossa operação:
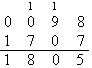 Note que, se os dois números a serem somados respeitarem o invariante
(isto é, se eles não tiverem zeros à esquerda),
o resultado também respeitará.
Note que, se os dois números a serem somados respeitarem o invariante
(isto é, se eles não tiverem zeros à esquerda),
o resultado também respeitará.
 Implemente as seguintes funções,
para operarem sobre dois números representados na base 10:
Implemente as seguintes funções,
para operarem sobre dois números representados na base 10: n
n definição de
definição de  definição de
definição de 
 def.
def.  def.
def.  indução
indução
 aritmética
aritmética
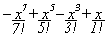 Usando a função do primeiro item,
calcule o valor desse polinômio para alguns valores de x entre 0 e 1.
Compare os valores obtidos com os de sin x.
Aumente o número de termos do seu polinômio
(aumentando n na função do item anterior),
e repita a comparação.
Usando a função do primeiro item,
calcule o valor desse polinômio para alguns valores de x entre 0 e 1.
Compare os valores obtidos com os de sin x.
Aumente o número de termos do seu polinômio
(aumentando n na função do item anterior),
e repita a comparação.
 Considere a função mostrada na figura 3.6,
onde
Considere a função mostrada na figura 3.6,
onde  12,
12,  23}
será representado pela lista
23}
será representado pela lista  8
8 16
16 ((x 1) (y 2) (z 5))
((x 1) (y 2) (z 5)) ((val 4) (y 2) (z 5))
((val 4) (y 2) (z 5)) ((x 6) (y 2) (z 5))
((x 6) (y 2) (z 5)) 13
13 65
65 1
1 Escrever os elementos de uma dada lista, dois por linha,
separados por um espaço.
Por exemplo, uma chamada como
Escrever os elementos de uma dada lista, dois por linha,
separados por um espaço.
Por exemplo, uma chamada como
 Conjuntos representados por listas.
Mostre os elementos entre chaves
Conjuntos representados por listas.
Mostre os elementos entre chaves  {3,10,9,5}
{3,10,9,5} 10100b
10100b 0b
0b valor em uma linha,
com um
valor em uma linha,
com um 
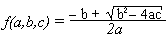
 Conjuntos representados por árvores de busca.
Mostre os elementos entre chaves
Conjuntos representados por árvores de busca.
Mostre os elementos entre chaves  {1,3,4,5,10,12}
{1,3,4,5,10,12} Repetidamente pedir um número ao usuário,
até este entrar com o número 0,
e retornar uma lista com todos os números lidos,
na mesma ordem em que eles foram dados.
Repetidamente pedir um número ao usuário,
até este entrar com o número 0,
e retornar uma lista com todos os números lidos,
na mesma ordem em que eles foram dados.
 3
3 19
19 (8 9)
(8 9) 4
4 Defina uma função que receba um vetor de números e
retorne a média aritmética entre o primeiro e o último elementos.
Defina uma função que receba um vetor de números e
retorne a média aritmética entre o primeiro e o último elementos.




 fim, pois
fim, pois  resultado final
resultado final Uma função que retorne uma lista com os elementos de um vetor.17
Uma função que retorne uma lista com os elementos de um vetor.17
 2
2 ()
() 19
19 Defina uma função
Defina uma função  3
3 0
0 (c u r s o)
(c u r s o) (i c c)
(i c c) Defina um procedimento
Defina um procedimento  #(() () () () () () () ())
#(() () () () () () () ()) #(9 10 13)
#(9 10 13) Escreva uma função
Escreva uma função  #(0 2 4 6 8)
#(0 2 4 6 8) #(1 1 1 1)
#(1 1 1 1)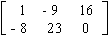
 Escreva uma função que receba dois parâmetros m e n
e retorne uma matriz de zeros de tamanho m × n.
Por exemplo
Escreva uma função que receba dois parâmetros m e n
e retorne uma matriz de zeros de tamanho m × n.
Por exemplo
 #(#(0 0) #(0 0) #(0 0))
#(#(0 0) #(0 0) #(0 0)) Escreva uma função
Escreva uma função  #(#(0 1 2) #(1 2 3) #(2 3 4))
#(#(0 1 2) #(1 2 3) #(2 3 4))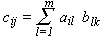
 definição de
definição de  valor de
valor de 


 definição de
definição de  valor de
valor de 




 1o lambda,
com {
1o lambda,
com { 4}
4} lambda, com {
lambda, com { 5}
5} aritmética
aritmética
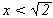 é o mesmo que testar
se x2 < 2; em Scheme:
é o mesmo que testar
se x2 < 2; em Scheme:
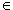 (5,10]. Portanto, o predicado
(5,10]. Portanto, o predicado 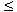 5),
ou que ele está acima (x>10).
Em Scheme,
5),
ou que ele está acima (x>10).
Em Scheme,  Exercício 3.17: Lembrando que as sub-árvores de uma
folha são árvores vazias, temos:
Exercício 3.17: Lembrando que as sub-árvores de uma
folha são árvores vazias, temos:
 Na representação pré-fixada, essa árvore resulta na lista
Na representação pré-fixada, essa árvore resulta na lista
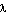 .
Essa notação para funções é baseada no
.
Essa notação para funções é baseada no
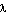 -cálculo, uma teoria criada na década de 40
pelo matemático A. Church.
Em uma notação mais `matemática',
a definição de
-cálculo, uma teoria criada na década de 40
pelo matemático A. Church.
Em uma notação mais `matemática',
a definição de 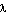 x . 2x.
(4)
Em várias implementações de Scheme,
a lista vazia
x . 2x.
(4)
Em várias implementações de Scheme,
a lista vazia